题目内容
【题目】求满足如下条件的最小正整数![]() :在
:在![]() 的圆周上任取
的圆周上任取![]() 个点
个点![]() ,则在
,则在![]() 个
个![]() 中,至少有2007个不超过
中,至少有2007个不超过![]() .
.
【答案】91
【解析】
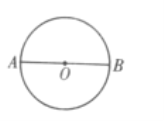
首先,当![]() 时,如图,设
时,如图,设![]() 是
是![]() 的直径,在点
的直径,在点![]() 和
和![]() 的附近分别取45个点,此时,只有
的附近分别取45个点,此时,只有![]() 个角不超过
个角不超过![]() .所以,
.所以,![]() 不满足题意.
不满足题意.
其次,当![]() 时,接下来证明:至少有2007个角不超过
时,接下来证明:至少有2007个角不超过![]() .
.
对圆周上的91个点![]() ,若
,若![]() ,则联结
,则联结![]() ,这样就得到一个图
,这样就得到一个图![]() .设图
.设图![]() 中有
中有![]() 条边.
条边.
当![]() ,
,![]() 时,
时,![]() ,故图
,故图![]() 中没有三角形.
中没有三角形.
若![]() ,则有
,则有![]() 个角不超过
个角不超过![]() ,命题得证.
,命题得证.
若![]() ,不妨设
,不妨设![]() 、
、![]() 之间有边相连,因为图中没有三角形,所以,对于点
之间有边相连,因为图中没有三角形,所以,对于点![]() ,它至多与
,它至多与![]() 、
、![]() 中的一个有边相连.从而,
中的一个有边相连.从而,![]() ,其中,
,其中,![]() 表示从
表示从![]() 处引出的边数.又
处引出的边数.又![]() ,而对图
,而对图![]() 中每一条边的两个顶点
中每一条边的两个顶点![]() 、
、![]() ,都有
,都有![]() .
.
于是,上式对每一条边求和可得![]() .
.
由柯西不等式得
![]()
![]() .
.
故![]()
![]() ,
,![]() .
.
因此,91个顶点中,至少有![]() 个点对,它们之间没有边相连.从而,对应的顶点所对应的角不超过
个点对,它们之间没有边相连.从而,对应的顶点所对应的角不超过![]() .
.
综上所述,![]() 的最小值为91.
的最小值为91.

练习册系列答案
相关题目