ĢāÄæÄŚČŻ
”¾ĢāÄæ”æøł¾ŻÄ³µē×ÓÉĢĪńĘ½Ģصĵ÷²éĶ³¼ĘĻŌŹ¾£¬²ĪÓėµ÷²éµÄ1 000Ī»ÉĻĶų¹ŗĪļÕßµÄÄźĮäĒéæöČēĶ¼ĖłŹ¾£®
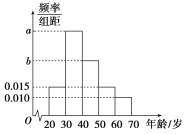
£Ø1£©ŅŃÖŖ[30£¬40£©£¬[40£¬50£©£¬[50£¬60£©ČżøöÄźĮä¶ĪµÄÉĻĶų¹ŗĪļÕßČĖŹż³ÉµČ²īŹżĮŠ£¬Ēó![]() µÄÖµ£»
掙术
£Ø2£©øƵē×ÓÉĢĪńĘ½Ģؽ«ÄźĮäŌŚ[30£¬50£©ÄŚµÄČĖČŗ¶ØŅåĪŖøßĻū·ŃČĖČŗ£¬ĘäĖūÄźĮä¶ĪµÄČĖČŗ¶ØŅåĪŖĒ±ŌŚĻū·ŃČĖČŗ£¬ĪŖĮĖ¹ÄĄųĒ±ŌŚĻū·ŃČĖČŗµÄĻū·Ń£¬øĆĘ½Ģؾö¶Ø·¢·Å“ś½šČÆ£¬øßĻū·ŃČĖČŗĆæČĖ·¢·Å50ŌŖµÄ“ś½šČÆ£¬Ē±ŌŚĻū·ŃČĖČŗĆæČĖ·¢·Å100ŌŖµÄ“ś½šČÆ£¬ĻÖ²ÉÓĆ·Ö²ć³éŃłµÄ·½Ź½“Ó²ĪÓėµ÷²éµÄ1 000Ī»ÉĻĶų¹ŗĪļÕßÖŠ³éČ”10ČĖ£¬²¢ŌŚÕā10ČĖÖŠĖ껜³éČ”3ČĖ½ųŠŠ»Ų·Ć£¬Ēó“Ė3ČĖ»ńµĆ“ś½šČÆ×ÜŗĶ![]() £Øµ„Ī»£ŗŌŖ£©µÄ·Ö²¼ĮŠÓėŹżŃ§ĘŚĶū£®
£Øµ„Ī»£ŗŌŖ£©µÄ·Ö²¼ĮŠÓėŹżŃ§ĘŚĶū£®
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©¼ū½āĪö
£»£Ø2£©¼ū½āĪö
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅā![]() ČżøöÄźĮä¶ĪµÄÉĻĶų¹ŗĪļÕßČĖŹż³ÉµČ²īŹżĮŠ£¬ĮŠ³ö·½³Ģ×飬¼“æÉĒó½ā£»
ČżøöÄźĮä¶ĪµÄÉĻĶų¹ŗĪļÕßČĖŹż³ÉµČ²īŹżĮŠ£¬ĮŠ³ö·½³Ģ×飬¼“æÉĒó½ā£»
£Ø2£©ĄūÓĆ·Ö²ć³éŃłµÄ·½·Ø£¬“ÓÖŠČ”³öČżČĖ£¬µĆ³öČżČĖĖł»ńµĆ“ś½šČƵÄ×ÜŗĶ![]() µÄȔֵ£¬ĒóµĆĻąÓ¦µÄøÅĀŹ£¬ĮŠ³ö·Ö²¼ĮŠ£¬ĄūÓĆĘŚĶūµÄ¹«Ź½£¬¼“æÉĒó½ā.
µÄȔֵ£¬ĒóµĆĻąÓ¦µÄøÅĀŹ£¬ĮŠ³ö·Ö²¼ĮŠ£¬ĄūÓĆĘŚĶūµÄ¹«Ź½£¬¼“æÉĒó½ā.
£Ø1£©ÓÉĢāŅāÖŖ![]() ČżøöÄźĮä¶ĪµÄÉĻĶų¹ŗĪļÕßČĖŹż³ÉµČ²īŹżĮŠ£¬
ČżøöÄźĮä¶ĪµÄÉĻĶų¹ŗĪļÕßČĖŹż³ÉµČ²īŹżĮŠ£¬
ĖłŅŌ![]() £¬½āµĆ
£¬½āµĆ![]() .
.
£Ø2£©ĄūÓĆ·Ö²ć³éŃł“ÓŃł±¾ÖŠ³éČ”10ČĖ£¬ĘäÖŠŹōÓŚøßĻū·ŃČĖČŗµÄĪŖ6ČĖŹōÓŚĒ±ŌŚĻū·ŃČĖČŗµÄĪŖ4ČĖ£¬“ÓÖŠČ”³öČżČĖ£¬²¢¼ĘĖćČżČĖĖł»ńµĆ“ś½šČƵÄ×ÜŗĶ![]() £¬
£¬
Ōņ![]() µÄĖłÓŠæÉÄÜȔֵĪŖ£ŗ
µÄĖłÓŠæÉÄÜȔֵĪŖ£ŗ![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
”ą![]() µÄ·Ö²¼ĮŠĪŖ
µÄ·Ö²¼ĮŠĪŖ
| 150 | 200 | 250 | 300 |
|
|
|
|
|
![]() .
.

 Č«ÓŵćĮ·µ„ŌŖ¼Ę»®ĻµĮŠ“š°ø
Č«ÓŵćĮ·µ„ŌŖ¼Ę»®ĻµĮŠ“š°ø”¾ĢāÄæ”æijĘóŅµÓŠĮ½øö·Ö³§Éś²śÄ³ÖÖĮć¼ž£¬°“¹ę¶ØÄŚ¾¶³ß“ē£Øµ„Ī»£ŗmm£©µÄÖµĀäŌŚ[29.94£¬30.06£©µÄĮć¼žĪŖÓÅÖŹĘ·.“ÓĮ½øö·Ö³§Éś²śµÄĮć¼žÖŠø÷³é³öĮĖ500¼ž£¬ĮæĘäÄŚ¾¶³ß“ē£¬µĆ½į¹ūČēĻĀ±ķ£ŗ
¼×³§£ŗ
·Ö×é | [29.86£¬29.90£© | [29.90£¬29.94£© | [29.94£¬29.98£© | [29.98£¬30.02£© | [30.02£¬30.06£© | [30.06£¬30.10£© | [30.10£¬30.14£© |
ʵŹż | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
ŅŅ³§£ŗ
·Ö×é | [29.86£¬29.90£© | [29.90£¬29.94£© | [29.94£¬29.98£© | [29.98£¬30.02£© | [30.02£¬30.06£© | [30.06£¬30.10£© | [30.10£¬30.14£© |
ʵŹż | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
£Ø1£©ŹŌ·Ö±š¹Ą¼ĘĮ½øö·Ö³§Éś²śµÄĮć¼žµÄÓÅÖŹĘ·ĀŹ£»
£Ø2£©ÓÉŅŌÉĻĶ³¼ĘŹż¾ŻĢīĻĀĆę![]() ĮŠĮŖ±ķ£¬²¢ĪŹŹĒ·ńÓŠ
ĮŠĮŖ±ķ£¬²¢ĪŹŹĒ·ńÓŠ![]() µÄ°ŃĪÕČĻĪŖ”°Į½øö·Ö³§Éś²śµÄĮć¼žµÄÖŹĮæÓŠ²īŅģ”±.
µÄ°ŃĪÕČĻĪŖ”°Į½øö·Ö³§Éś²śµÄĮć¼žµÄÖŹĮæÓŠ²īŅģ”±.
¼× ³§ | ŅŅ ³§ | ŗĻ¼Ę | |
ÓÅÖŹĘ· | |||
·ĒÓÅÖŹĘ· | |||
ŗĻ¼Ę |
ø½£ŗ 
|
|
|
|
|
|
|
|
|
|