题目内容
【题目】已知![]() 为抛物线
为抛物线![]() 上的两个动点,点
上的两个动点,点![]() 在第一象限,点
在第一象限,点![]() 在第四象限,
在第四象限,![]() 分别过点
分别过点![]() 且与抛物线
且与抛物线![]() 相切,
相切,![]() 为
为![]() 的交点.
的交点.
(Ⅰ)若直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,求证动点
,求证动点![]() 在一条定直线上,并求此直线方程;
在一条定直线上,并求此直线方程;
(Ⅱ)设![]() 为直线
为直线![]() 与直线
与直线![]() 的交点,求
的交点,求![]() 面积的最小值.
面积的最小值.
【答案】(Ⅰ)证明见解析,![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题(I)利用直线![]() 与抛物线
与抛物线![]() 相切,求出
相切,求出![]() 方程,可得点
方程,可得点![]() 坐标,再求出直线
坐标,再求出直线![]() 的方程,即要得结论;(II)求出
的方程,即要得结论;(II)求出![]() 的坐标,可得
的坐标,可得![]() ,表示
,表示![]() 面积,利用导数法可求最小值.
面积,利用导数法可求最小值.
试题解析:(Ⅰ)设![]() .
.
易知![]() 斜率存在,设为
斜率存在,设为![]() ,则方程为
,则方程为![]()
由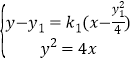 ,得
,得![]() ……①
……①
由直线![]() 与抛物线
与抛物线![]() 相切,知
相切,知![]() .
.
于是![]() ,
,![]() 方程为
方程为![]() .
.
同理,![]() 方程为
方程为![]() .
.
联立![]() 、
、![]() 方程可得点
方程可得点![]() 坐标为
坐标为![]() ,
,
∵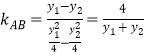 ,
,![]() 方程为
方程为![]() ,
,![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,点
,点![]() 在一条定直线
在一条定直线![]() 上.
上.
或解:设![]() ,则
,则![]() 方程为
方程为![]() ,
,![]() 方程为
方程为![]() .
.
点![]() 坐标满足方程
坐标满足方程![]() ,
,
∴直线![]() 方程为
方程为![]() ,由直线
,由直线![]() 过点
过点![]() ,知
,知![]() ,
,
∴![]() ,点
,点![]() 在定直线
在定直线![]() 上
上
(Ⅱ)由(Ⅰ)知![]() 的坐标分别为
的坐标分别为![]() ,
,
![]() .
.
设![]() .
.
由![]() 知
知![]() ,
,
当且仅当![]() 时等号成立.
时等号成立.
∴![]() .
.
设![]() ,则
,则![]() .
.
∴![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
![]() 在区间
在区间![]() 上为减函数,在区间
上为减函数,在区间![]() 上为增函数.
上为增函数.
∴![]() 时,
时,![]() 取最小值
取最小值![]() .
.
∴当![]() ,即
,即![]() 时,
时,
![]() 面积取最小值
面积取最小值![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目