Question

【题目】已知点与点都在椭圆上，且的左集点为，过点的直线交椭圆于，两点.

（1）求的方程；

（2）若以为直径的圆经过点，求直线的方程.

Answer 1

【答案】（1）；（2）或.

【解析】

（1）利用点在曲线上，列出方程组求解即可求出椭圆的方程．

（2）依题意可知直线AB的斜率存在，设为k，则直线AB的方程为，

设点，.消元列出韦达定理及判别式，若以AB为直径的圆经过点，则，则，从而计算可得；

解：（1）由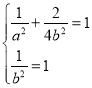得，，

椭圆C的方程为.

（2）点.显然直线AB的斜率存在，设为k，

则直线AB的方程为，

设点，.

联立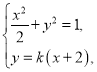消去y得，

故，

所以.（*）

且，.

所以直线，的斜率分别为，.

若以AB为直径的圆经过点，则.

则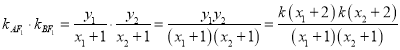

，

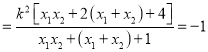得，

则，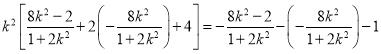

化简得，解得.

因为都满足（*）式，

所以直线AB的方程为或.

即直线AB的方程为或.