题目内容
20.已知向量$\overrightarrow{a}$的终点与向量$\overrightarrow{b}$的起点重合,向量$\overrightarrow{c}$的起点与向量$\overrightarrow{b}$的终点重合,则下列结论中,正确的个数为( )①以$\overrightarrow{a}$的起点为终点,以$\overrightarrow{c}$的起点为起点的向量为-($\overrightarrow{a}+\overrightarrow{b}$)
②以$\overrightarrow{a}$的起点为终点,以$\overrightarrow{c}$的终点为起点的向量为-$\overrightarrow{a}-\overrightarrow{b}-\overrightarrow{c}$
③以$\overrightarrow{b}$的起点为终点,以$\overrightarrow{c}$的终点为起点的向量为-$\overrightarrow{b}-\overrightarrow{c}$.
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
分析 如图所示,作$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}=\overrightarrow{c}$.可得:①$\overrightarrow{CA}$=$\overrightarrow{CB}+\overrightarrow{BA}$;②$\overrightarrow{DA}$=$\overrightarrow{DC}+\overrightarrow{CB}+\overrightarrow{BA}$;③$\overrightarrow{DB}$=$\overrightarrow{DC}+\overrightarrow{CB}$.即可判断出正误.
解答 解:如图所示,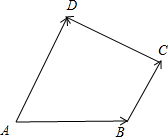
作$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}=\overrightarrow{c}$.
①$\overrightarrow{CA}$=$\overrightarrow{CB}+\overrightarrow{BA}$=$-(\overrightarrow{b}+\overrightarrow{a})$,正确;
②$\overrightarrow{DA}$=$\overrightarrow{DC}+\overrightarrow{CB}+\overrightarrow{BA}$=$-\overrightarrow{c}-\overrightarrow{b}-\overrightarrow{a}$,正确;
③$\overrightarrow{DB}$=$\overrightarrow{DC}+\overrightarrow{CB}$=-$\overrightarrow{c}-\overrightarrow{b}$,正确.
综上可得:正确命题的个数为:3.
故选:C.
点评 本题考查了向量的三角形法则与多边形法则,属于基础题.

| A. | (-2,+∞) | B. | (-2,$\sqrt{2}+1$) | C. | (-∞,$\sqrt{2}+1$) | D. | (-$\sqrt{2}+1$,$\sqrt{2}+1$) |