题目内容
【题目】已知函数![]() (
(![]() ),
),![]() .
.
(1)当![]() 时,
时,![]() 与
与![]() 在定义域上的单调性相反,求b的取值范围;
在定义域上的单调性相反,求b的取值范围;
(2)设![]() ,
,![]() 是函数
是函数![]() 的两个零点,且
的两个零点,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据导数判断g(x)的单调性,然后再分析f(x)中b的取值范围;(2)先分别表示出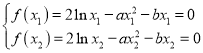 ,再利用做差得
,再利用做差得![]() ,将其化简为:
,将其化简为:![]() ;根据要证明的式子:我们可化为
;根据要证明的式子:我们可化为![]()
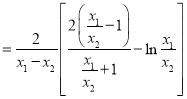 ,再结合g(x)的性质,判断函数值的正负即可
,再结合g(x)的性质,判断函数值的正负即可
(1)∵![]() ,
,
∴![]()
由题意可知,![]() 与
与![]() 的定义域均为
的定义域均为![]() ,
,
∵ ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
又![]() 时,
时,![]() 与
与![]() 在定义域上的单调性相反,
在定义域上的单调性相反,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
∴只需![]() ,
,
∵![]() ,
,
∴![]() (当且仅当
(当且仅当![]() 时,等号成立),
时,等号成立),
∴![]() ,
,
∴b的取值范围![]() ;
;
(2)由已知可得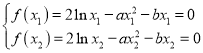 ,
,
∴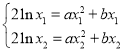 ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
从而![]()
![]()
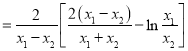
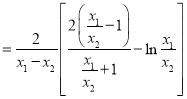 ,
,
![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
即![]() ,
,
即证.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某汽车公司为调查4S店个数对该公司汽车销量的影响,对同等规模的A,B,C,D四座城市的4S店一个月某型号汽车销量进行了统计,结果如下表:
城市 | A | B | C | D |
4S店个数x | 3 | 4 | 6 | 7 |
销售台数y | 18 | 26 | 34 | 42 |
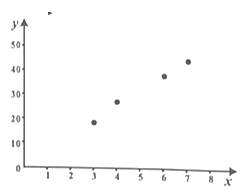
(1)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程;
(2)根据统计每个城市汽车的盈利![]() (万元)与该城市4S店的个数x符合函数
(万元)与该城市4S店的个数x符合函数![]() ,
,![]() ,为扩大销售,该公司在同等规模的城市E预计要开设多少个4S店,才能使E市的4S店一个月某型号骑车销售盈利达到最大,并求出最大值.
,为扩大销售,该公司在同等规模的城市E预计要开设多少个4S店,才能使E市的4S店一个月某型号骑车销售盈利达到最大,并求出最大值.
附:回归方程![]() 中的斜率和截距的最小二乘法估计公式分别为:
中的斜率和截距的最小二乘法估计公式分别为: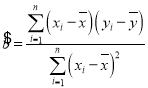 ,
,![]()