题目内容
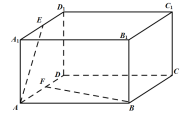
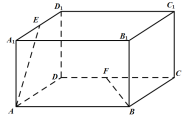
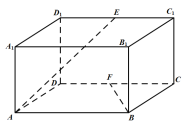
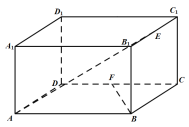
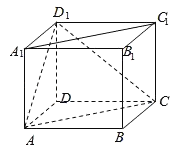
【题目】如图,在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形.
(1)证明:A1C1![]() 平面ACD1;
平面ACD1;
(2)求异面直线CD与AD1所成角的大小;
(3)已知三棱锥D1﹣ACD的体积为![]() ,求AA1的长.
,求AA1的长.
【答案】(1)见解析(2)90°(3)AA1=1.
【解析】
(1)先证明A1C1![]() AC,即得证;
AC,即得证;
(2)由CD⊥平面ADD1A1,可得CD⊥AD1,即得解;
(3)由![]() ,AA1的长可看作三棱锥D1﹣ACD的高,利用体积即得解.
,AA1的长可看作三棱锥D1﹣ACD的高,利用体积即得解.
(1)证明:在长方体中,因A1A=CC1,A1A![]() CC1,可得A1C1
CC1,可得A1C1![]() AC,
AC,
A1C1不在平面ACD1内,AC平面ACD1,
则A1C1![]() 平面ACD1;
平面ACD1;
(2)解:因为CD⊥平面ADD1A1,AD1平面ADD1A1,可得CD⊥AD1,
所以异面直线CD与AD1所成角90°
(3)解:由三棱锥D1﹣ACD的体积为![]() ,
,
由于![]() 平面ACD,且
平面ACD,且![]()
可得![]() ,
,
∴AA1=1.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目