Question

【题目】如图，在四校锥P﹣ABCD中，底面ABCD是菱形，∠BAD＝60°，边长为4的正△PAD所在平面与平面ABCD垂直，点E是AD的中点，点Q是侧棱PC的中点．

（1）求四棱锥P﹣ABCD的体积；

（2）求证：PA∥平面BDQ；

（3）在线段AB上是否存在点F，使直线PF与平面PAD所成的角为30°？若存在，求出AF的长，若不存在，请说明理由？

Answer 1

【答案】（1）16；（2）见解析；（3）存在，AF

【解析】

（1）根据底面ABCD是菱形，且∠BAD＝60°，边长为4，求面积，再由正△PAD所在平面与平面ABCD垂直，，得到平面ABCD，PE是底面上的高，然后代入体积公式求解.

（2）由O是AC中点，点Q是侧棱PC的中点，根据中位线得到OQ∥PA，再利用线面平行的判定理证明.

（3）建立空间直角坐标系，设在线段AB上存在点F，且，求得相应点的坐标，进而得到向量的坐标，再利用直线PF与平面PAD所成的角为30°，代入线面角的向量法公式求解.

（1）

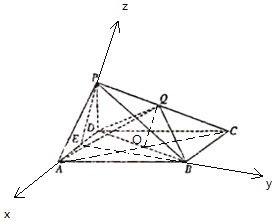
如图所示：连结PE，BE，

∵在四棱锥P﹣ABCD中，底面ABCD是菱形，∠BAD＝60°，边长为4，

∴S四边形ABCD＝AD×BE＝48，

又因为正△PAD所在平面与平面ABCD垂直，

所以平面ABCD，

又PE2，

∴四棱锥P﹣ABCD的体积：VP﹣ABCD16．

（2）证明：连结AC，BD，交于点O，连结OQ，

∵底面ABCD是菱形，∴O是AC中点，

∵点Q是侧棱PC的中点，

∴OQ∥PA，∵PA平面BDQ，OQ平面BDQ，

∴PA∥平面BDQ．

（3）以E为原点，EA为x轴，EB为y轴，EP为z轴，建立空间直角坐标系，

A（2，0，0），B（0，2，0），P（0，0，2），

设在线段AB上存在点F，使直线PF与平面PAD所成的角为30°，

且F（a，b，c），，即（a﹣2，b，c）＝（﹣2λ，2，0），λ∈[0，1]，

即a＝2﹣2λ，b＝2λ，c＝0，∴F（2﹣2λ，2，0），

因为平面PAD的法向量（0，1，0），

（2﹣2，﹣2），且直线PF与平面PAD所成的角为30°，

∴sin30°，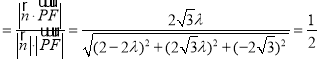

解得，符合λ∈[0，1]，

∴AF＝λAB．

∴在线段AB上存在点F，使直线PF与平面PAD所成的角为30°，且AF．