题目内容
【题目】某城市通过抽样调查的方法获得了100户居民某月用水量(单位:t)的频率分布直方图:
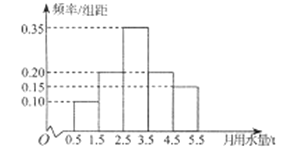
(Ⅰ)求这100户居民该月用水量的平均值;
(Ⅱ)从该月用水量在![]() 和
和![]() 两个区间的用户中,用分层抽样的方法邀请5户的户主共5人参加水价调整方案听证会,现从这5人中随机选取2人在会上进行陈述发言,求选取的2人均来自用水量低于2.5t的用户的概率.
两个区间的用户中,用分层抽样的方法邀请5户的户主共5人参加水价调整方案听证会,现从这5人中随机选取2人在会上进行陈述发言,求选取的2人均来自用水量低于2.5t的用户的概率.
【答案】(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)![]()
【解析】
(Ⅰ)通过频率分布直方图可计算该市居民每月用水量的平均数;
(Ⅱ)求出月平均用水量为![]() 和
和![]() 内的用户,计算分层抽样抽取比例, 即可求出月平均用水量在
内的用户,计算分层抽样抽取比例, 即可求出月平均用水量在![]() 和
和![]() 的用户中应抽取的户数,然后再根据古典概型,即可求出结果.
的用户中应抽取的户数,然后再根据古典概型,即可求出结果.
(Ⅰ)由题意可知,这100户居民该月用水量的平均值为:
![]() ;
;
(Ⅱ)由题意可知,
月平均用水量为![]() 内的用户有
内的用户有![]() 户,
户,
月平均用水在![]() 内的用户有
内的用户有![]() 户,
户,
用分层抽样的方法抽取![]() 户,抽取比例为
户,抽取比例为![]() ,
,
所以月平均用水量在![]() 的用户中应抽取
的用户中应抽取![]() 户,设这三户分别为
户,设这三户分别为![]() ;
;
月平均用水量在![]() 的用户中应抽取
的用户中应抽取![]() 户, 设这三户分别为
户, 设这三户分别为![]() ;
;
从这5人中随机选取2人在会上进行陈述发言共有:![]() 10种情况,其中选取的2人均来自用水量低于2.5t的用户共有3种情况,所以选取的2人均来自用水量低于2.5t的用户的概率为
10种情况,其中选取的2人均来自用水量低于2.5t的用户共有3种情况,所以选取的2人均来自用水量低于2.5t的用户的概率为![]() .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】某医院治疗白血病有甲、乙两套方案,现就70名患者治疗后复发的情况进行了统计,得到其等高条形图如图所示(其中采用甲、乙两种治疗方案的患者人数之比为![]() .
.
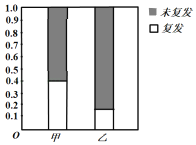
(1)补充完整![]() 列联表中的数据,并判断是否有
列联表中的数据,并判断是否有![]() 把握认为甲乙两套治疗方案对患者白血病复发有影响;
把握认为甲乙两套治疗方案对患者白血病复发有影响;
复发 | 未复发 | 总计 | |
甲方案 | |||
乙方案 | 2 | ||
总计 | 70 |
(2)为改进“甲方案”,按分层抽样组成了由5名患者构成的样本,求随机抽取2名患者恰好是复发患者和未复发患者各1名的概率.
附:
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 |
![]() ,
,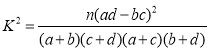 .
.
【题目】“五一”期间,甲乙两个商场分别开展促销活动.
(Ⅰ)甲商场的规则是:凡购物满100元,可抽奖一次,从装有大小、形状相同的4个白球、4个黑球的袋中摸出4个球,中奖情况如下表:
摸出的结果 | 获得奖金(单位:元) |
4个白球或4个黑球 | 200 |
3个白球1个黑球或3个黑球1个白球 | 20 |
2个黑球2个白球 | 10 |
记![]() 为抽奖一次获得的奖金,求
为抽奖一次获得的奖金,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)乙商场的规则是:凡购物满100元,可抽奖10次.其中,第![]() 次抽奖方法是:从编号为
次抽奖方法是:从编号为![]() 的袋中(装有大小、形状相同的
的袋中(装有大小、形状相同的![]() 个白球和
个白球和![]() 个黑球)摸出
个黑球)摸出![]() 个球,若该次摸出的
个球,若该次摸出的![]() 个球颜色都相同,则可获得奖金
个球颜色都相同,则可获得奖金![]() 元;记第
元;记第![]() 次获奖概率
次获奖概率![]() .设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
.设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
①求证:![]() ;
;
②若某顾客购买120元的商品,不考虑其它因素,从获得奖金的期望分析,他应该选择哪一家商场?