题目内容
10．若抛物线y2=8ax的焦点与双曲线$\frac{x^2}{a^2}-{y^2}$=1的右焦点重合，则双曲线的离心率为2．分析 求出抛物线的焦点坐标，然后求解双曲线的离心率．
解答 解：抛物线y2=8ax的焦点（2a，0），抛物线y2=8ax的焦点与双曲线$\frac{x^2}{a^2}-{y^2}$=1的右焦点（c，0）重合，
可得2a=c，
双曲线的离心率为：$\frac{c}{a}=2$
故答案为：2．
点评 本题考查抛物线的简单性质，双曲线的离心率的求法，考查计算能力．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
1．已知函数f（x）=cos（2x-$\frac{π}{3}$），g（x）=sin2x，将函数f（x）的图象经过下列哪种可以与g（x） 的图象重合（ ）
| A． | 向左平移$\frac{π}{12}$个单位 | B． | 向左平移$\frac{π}{6}$个单位 | ||
| C． | 向右平移$\frac{π}{12}$个单位 | D． | 向右平移$\frac{π}{6}$个单位 |
2．阅读下面程序框图，为使输出的数据为11，则①处应填的数字可以为（ ）
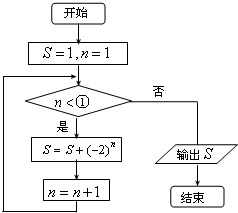
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |