题目内容
11.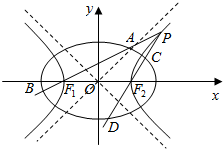 如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.
如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.(1)求椭圆和双曲线的标准方程;(2)设直线PF1,PF2的斜率分别为k1,k2,探求k1与k2的关系;
(3)是否存在常数λ,使得|AB|+|CD|=λ|AB||CD|恒成立?若存在,求出λ的值;若不存在,请说明理由.
分析 (1)由题意知,椭圆中:4a=8$\sqrt{2}$,$\frac{1}{2}×2a×2b$=8$\sqrt{2}$,解出即可得椭圆的方程;又顶点与焦点重合,可得m=c2=a2-b2.可得该双曲线的标准方程.
(2)设点P(x,y)(x≠±2),利用斜率计算公式可得:${k}_{1}=\frac{y}{x+2}$,k2=$\frac{y}{x-2}$,k1•k2=$\frac{{y}^{2}}{{x}^{2}-4}$.由P在双曲线上,可得x2-y2=4,代入即可得出.
(3)设直线AB:y=k1(x+2)(k1≠0),与椭圆方程联立化为$(2{k}_{1}^{2}+1){x}^{2}$+$8{k}_{1}^{2}x$+$8{k}_{1}^{2}$-8=0,设A(x1,y1),B(x2,y2).利用弦长公式|AB|=$\sqrt{(1+{k}_{1}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\frac{4\sqrt{2}(1+{k}_{1}^{2})}{2{k}_{1}^{2}+1}$,同理|CD|=$\frac{4\sqrt{2}(1+{k}_{2}^{2})}{2{k}_{2}^{2}+1}$,由k1•k2=1,代入|AB|+|CD|=λ|AB||CD|,可得λ为常数.
解答 解:(1)由题意知,椭圆中:4a=8$\sqrt{2}$,$\frac{1}{2}×2a×2b$=8$\sqrt{2}$,
解得a=2$\sqrt{2}$,b=2.
∴椭圆的标准方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1.
又顶点与焦点重合,∴m=c2=a2-b2=4.
∴该双曲线的标准方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}$=1.
(2)设点P(x,y)(x≠±2),${k}_{1}=\frac{y}{x+2}$,k2=$\frac{y}{x-2}$,k1•k2=$\frac{{y}^{2}}{{x}^{2}-4}$.
∵P在双曲线上,∴x2-y2=4,∴y2=x2-4.
∴k1•k2=1.
(3)设直线AB:y=k1(x+2)(k1≠0),
联立$\left\{\begin{array}{l}{y={k}_{1}(x+2)}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,化为$(2{k}_{1}^{2}+1){x}^{2}$+$8{k}_{1}^{2}x$+$8{k}_{1}^{2}$-8=0,
设A(x1,y1),B(x2,y2).
∴x1+x2=$\frac{-8{k}_{1}^{2}}{2{k}_{1}^{2}+1}$,x1x2=$\frac{8{k}_{1}^{2}-8}{2{k}_{1}^{2}+1}$,
由弦长公式|AB|=$\sqrt{(1+{k}_{1}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\frac{4\sqrt{2}(1+{k}_{1}^{2})}{2{k}_{1}^{2}+1}$,
同理|CD|=$\frac{4\sqrt{2}(1+{k}_{2}^{2})}{2{k}_{2}^{2}+1}$,
由k1•k2=1,可得${k}_{2}=\frac{1}{{k}_{1}}$,代入上式可得:|CD|=$\frac{4\sqrt{2}(1+{k}_{1}^{2})}{{k}_{1}^{2}+2}$,
由|AB|+|CD|=λ|AB||CD|,可得λ=$\frac{1}{|AB|}+\frac{1}{|CD|}$=$\frac{3\sqrt{2}}{8}$,
∴存在常数λ=$\frac{3\sqrt{2}}{8}$,使得|AB|+|CD|=λ|AB||CD|恒成立.
点评 本题考查了椭圆与双曲线的坐标方程及其性质、直线与椭圆双曲线相交问题转化为方程联立可得根与系数的关系、弦长公式、斜率计算公式,考查了推理能力与计算能力,属于难题.

| A. | (-10,13) | B. | (9,-12) | C. | (-5,7) | D. | (5,-7) |
| A. | [-1,$\frac{1}{2}$) | B. | [-2,$\frac{1}{2}$) | C. | [-2,$\frac{3}{2}$) | D. | [-1,$\frac{3}{2}$) |
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | b<a<c |
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
| A. | 开口向上,焦点为(0,1) | B. | 开口向右,焦点为(1,0) | ||
| C. | 开口向上,焦点为(0,$\frac{1}{16}$) | D. | 开口向右,焦点为($\frac{1}{16}$,0) |