题目内容
13.将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则( )| A. | 对任意的a,b,e1>e2 | B. | 当a>b时,e1>e2;当a<b时,e1<e2 | ||
| C. | 对任意的a,b,e1<e2 | D. | 当a>b时,e1<e2;当a<b时,e1>e2 |
分析 分别求出双曲线的离心率,再平方作差,即可得出结论.
解答 解:由题意,双曲线C1:c2=a2+b2,e1=$\frac{c}{a}$;
双曲线C2:c′2=(a+m)2+(b+m)2,e2=$\frac{\sqrt{(a+m)^{2}+(b+m)^{2}}}{a+m}$,
∴${{e}_{1}}^{2}-{{e}_{2}}^{2}$=$\frac{{b}^{2}}{{a}^{2}}$-$\frac{(b+m)^{2}}{(a+m)^{2}}$=$\frac{(b-a)(2abm+b{m}^{2}+a{m}^{2})}{{a}^{2}(a+m)^{2}}$,
∴当a>b时,e1<e2;当a<b时,e1>e2,
故选:D.
点评 本题考查双曲线的性质,考查学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知A,B为双曲线E的左,右顶点,点M在E上,△ABM为等腰三角形,顶角为120°,则E的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
4.设集合M={x|x2=x},N={x|lgx≤0},则M∪N=( )
| A. | [0,1] | B. | (0,1] | C. | [0,1) | D. | (-∞,1] |
1.设D为△ABC所在平面内一点,$\overrightarrow{BC}=3\overrightarrow{CD}$,则( )
| A. | $\overrightarrow{AD}=-\frac{1}{3}\overrightarrow{AB}+\frac{4}{3}\overrightarrow{AC}$ | B. | $\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}-\frac{4}{3}\overrightarrow{AC}$ | C. | $\overrightarrow{AD}=\frac{4}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | D. | $\overrightarrow{AD}=\frac{4}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AC}$ |
8.命题“?x0∈(0,+∞),lnx0=x0-1”的否定是( )
| A. | ?x0∈(0,+∞),lnx0≠x0-1 | B. | ?x0∉(0,+∞),lnx0=x0-1 | ||
| C. | ?x∈(0,+∞),lnx≠x-1 | D. | ?x∉(0,+∞),lnx=x-1 |
2.阅读如图的程序框图,运行相应的程序,则输出S的值为( )
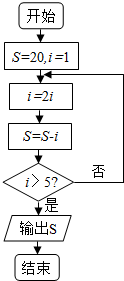

| A. | -10 | B. | 6 | C. | 14 | D. | 18 |
5.从1,2,3,4,5中有放回的依次取出两个数,则下列各对事件中是互斥事件的是( )
| A. | 恰有1个是奇数和全是奇数 | B. | 恰有1个是偶数和至少有1个是偶数 | ||
| C. | 至少有1个是奇数和全是奇数 | D. | 至少有1个是偶数和全是偶数 |
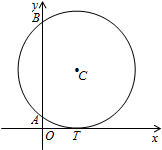 如图,已知圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.
如图,已知圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.