题目内容
1.设D为△ABC所在平面内一点,$\overrightarrow{BC}=3\overrightarrow{CD}$,则( )| A. | $\overrightarrow{AD}=-\frac{1}{3}\overrightarrow{AB}+\frac{4}{3}\overrightarrow{AC}$ | B. | $\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}-\frac{4}{3}\overrightarrow{AC}$ | C. | $\overrightarrow{AD}=\frac{4}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | D. | $\overrightarrow{AD}=\frac{4}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AC}$ |
分析 将向量$\overrightarrow{AD}$利用向量的三角形法则首先表示为$\overrightarrow{AB}+\overrightarrow{BD}$,然后结合已知表示为$\overrightarrow{AB},\overrightarrow{AC}$的形式.
解答 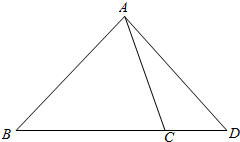 解:由已知得到如图
解:由已知得到如图
由$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}$=$\overrightarrow{AB}+\frac{4}{3}\overrightarrow{BC}$=$\overrightarrow{AB}+\frac{4}{3}(\overrightarrow{AC}-\overrightarrow{AB})$=$-\frac{1}{3}\overrightarrow{AB}+\frac{4}{3}\overrightarrow{AC}$;
故选:A.
点评 本题考查了向量的三角形法则的运用;关键是想法将向量$\overrightarrow{AD}$表示为$\overrightarrow{AB},\overrightarrow{AC}$.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.对任意向量$\overrightarrow{a}$、$\overrightarrow{b}$,下列关系式中不恒成立的是( )
| A. | |$\overrightarrow{a}•\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | B. | |$\overrightarrow{a}-\overrightarrow{b}$|≤||$\overrightarrow{a}$|-|$\overrightarrow{b}$|| | C. | ($\overrightarrow{a}+\overrightarrow{b}$)2=|$\overrightarrow{a}+\overrightarrow{b}$|2 | D. | ($\overrightarrow{a}+\overrightarrow{b}$)•($\overrightarrow{a}-\overrightarrow{b}$)=$\overrightarrow{a}$2-$\overrightarrow{b}$2 |
6.i为虚数单位,i607=( )
| A. | -i | B. | i | C. | 1 | D. | -1 |
13.将离心率为e1的双曲线C1的实半轴长a和虚半轴长b(a≠b)同时增加m(m>0)个单位长度,得到离心率为e2的双曲线C2,则( )
| A. | 对任意的a,b,e1>e2 | B. | 当a>b时,e1>e2;当a<b时,e1<e2 | ||
| C. | 对任意的a,b,e1<e2 | D. | 当a>b时,e1<e2;当a<b时,e1>e2 |
