题目内容

5．已知a≥b＞0，求证：2a3-b3≥2ab2-a2b．

分析 直接利用作差法，然后分析证明即可．

解答 证明：2a3-b3-2ab2+a2b=2a（a2-b2）+b（a2-b2）=（a-b）（a+b）（2a+b），
∵a≥b＞0，∴a-b≥0，a+b＞0，2a+b＞0，
从而：（a-b）（a+b）（2a+b）≥0，
∴2a3-b3≥2ab2-a2b．

点评 本题考查不等式的证明，作差法的应用，考查逻辑推理能力．

练习册系列答案
相关题目
15．△ABC是边长为2的等边三角形，已知向量$\vec a、\vec b$满足$\overrightarrow{AB}$=2$\overrightarrow{a}$，$\overrightarrow{AC}$=2$\overrightarrow{a}$+$\overrightarrow{b}$，则下列结论中正确的是①④⑤．（写出所有正确结论得序号）
①$\vec a$为单位向量；②$\vec b$为单位向量；③$\vec a⊥\vec b$；④$\overrightarrow{b}$∥$\overrightarrow{BC}$；⑤（4$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{BC}$．
16．设fn（x）是等比数列1，x，x2，…，xn的各项和，其中x＞0，n∈N，n≥2．
（Ⅰ）证明：函数Fn（x）=fn（x）-2在（$\frac{1}{2}$，1）内有且仅有一个零点（记为xn），且xn=$\frac{1}{2}$+$\frac{1}{2}$x${\;}_{n}^{n+1}$；
（Ⅱ）设有一个与上述等比数列的首项、末项、项数分别相同的等差数列，其各项和为gn（x），比较fn（x）和gn（x）的大小，并加以证明．
13．将离心率为e1的双曲线C1的实半轴长a和虚半轴长b（a≠b）同时增加m（m＞0）个单位长度，得到离心率为e2的双曲线C2，则（　　）
A．对任意的a，b，e1＞e2B．当a＞b时，e1＞e2；当a＜b时，e1＜e2
C．对任意的a，b，e1＜e2D．当a＞b时，e1＜e2；当a＜b时，e1＞e2
20．设等差数列{an}的公差为d，前n项和为Sn，等比数列{bn}的公比为q，已知b1=a1，b2=2，q=d，S10=100．
（1）求数列{an}，{bn}的通项公式
（2）当d＞1时，记cn=$\frac{a_n}{b_n}$，求数列{cn}的前n项和Tn．
10．如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为14，18，则输出的a=（　　）
A．0B．2C．4D．14
17．如图，长方体ABCD-A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4．过E，F的平面α与此长方体的面相交，交线围成一个正方形
（Ⅰ）在图中画出这个正方形（不必说出画法和理由）
（Ⅱ）求平面α把该长方体分成的两部分体积的比值．
14．已知函数f（x）=nx-xn，x∈R，其中n∈N•，且n≥2．
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）设曲线y=f（x）与x轴正半轴的交点为P，曲线在点P处的切线方程为y=g（x），求证：对于任意的正实数x，都有f（x）≤g（x）；
（Ⅲ）若关于x的方程f（x）=a（a为实数）有两个正实数根x1，x2，求证：|x2-x1|＜$\frac{a}{1-n}$+2．
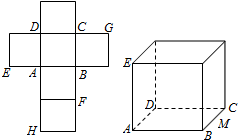17．一个正方体的平面展开图及该正方体的直观图的示意图如图所示．在正方体中，设BC的中点为M、GH的中点为N．
（Ⅰ）请将字母F、G、H标记在正方体相应的顶点处（不需说明理由）；
（Ⅱ）证明：直线MN∥平面BDH；
（Ⅲ）求二面角A-EG-M的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网