题目内容
13.在△ABC中,内角A,B,C的对边分别是a,b,c,若$\frac{a}{b}=\frac{b+\sqrt{3}c}{a}$,sinC=2$\sqrt{3}$sinB,则tanA$\frac{\sqrt{3}}{3}$.分析 利用正弦定理求得和已知等式分别求得b和c,b和a的关系,最后利用余弦定理求得cosA的值,求得A,则tanA可求得.
解答 解:∵sinC=2$\sqrt{3}$sinB,
∴c=2$\sqrt{3}$b,
∴$\frac{a}{b}=\frac{b+\sqrt{3}c}{a}$=$\frac{b+6b}{a}$,
∴a2=7b2,
cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{{b}^{2}+12{b}^{2}-7{b}^{2}}{4\sqrt{3}{b}^{2}}$=$\frac{\sqrt{3}}{2}$,
∴A=$\frac{π}{6}$,
∴tanA=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题主要考查了正弦定理和余弦定理的运用.正弦定理和余弦定理是解三角形问题常用公式,应能熟练和灵活运用.

练习册系列答案
相关题目
1.某中学为了研究学生的视力和座位(有关和无关)的关系,运用2×2列联表进行独立性研究,经计算K2=7.069,则至少有( )的把握认为“学生的视力与座位有关”.
附:
附:
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 95% | B. | 99% | C. | 97.5% | D. | 90% |
8.已知函数f(x)是奇函数,且当x>0时,f(x)=ex,则f(-1)=( )
| A. | $\frac{1}{e}$ | B. | -$\frac{1}{e}$ | C. | e | D. | -e |
18.已知函数f(x)的定义域为实数R,f′(x)是其导函数,对任意实数x有f(x)+xf′(x)>0,则当a>b时,下列不等式成立的是( )
| A. | af(b)>bf(a) | B. | af(a)>bf(b) | C. | bf(a)>af(b) | D. | bf(b)>af(a) |
5.甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
乙校:
(Ⅰ)计算x,y的值;
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率;
(Ⅲ)由以上统计数据填写右面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 3 | 10 | 15 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 9 | 8 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率;
(Ⅲ)由以上统计数据填写右面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
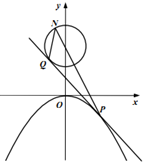 如图,曲线C1:x2=-4y,曲线C2:x2+(y-m)2=1(m>0),过曲线C1上的一点P(2,-1)作曲线C1的切线l,且l与C2恰好相切,切点为Q.
如图,曲线C1:x2=-4y,曲线C2:x2+(y-m)2=1(m>0),过曲线C1上的一点P(2,-1)作曲线C1的切线l,且l与C2恰好相切,切点为Q.