题目内容
4.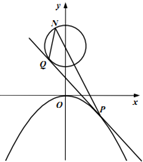 如图,曲线C1:x2=-4y,曲线C2:x2+(y-m)2=1(m>0),过曲线C1上的一点P(2,-1)作曲线C1的切线l,且l与C2恰好相切,切点为Q.
如图,曲线C1:x2=-4y,曲线C2:x2+(y-m)2=1(m>0),过曲线C1上的一点P(2,-1)作曲线C1的切线l,且l与C2恰好相切,切点为Q.(Ⅰ)求曲线C2与直线l的方程;
(Ⅱ)若点N为C2上任意一异于Q的动点,求△NPQ面积的最大值.
分析 (Ⅰ)设出直线l的方程,联立方程组,根据直线和圆相切,得到判别式△=0,解出k的值,从而求出直线l的方程,再根据直线l和c2相切,得到距离d=1,从而求出c2方程;
(Ⅱ)设出Q的坐标,联立方程,求出Q的坐标,从而求出|PQ|的长,设d为点N到直线PQ的距离,则S△NPQ=$\frac{|PQ|}{2}$d,显然d的最大值为圆的直径,即点N与点Q位于直径的两端,从而求出三角形面积的最大值.
解答 解:(Ⅰ)由题意得:直线l的斜率显然存在,
设直线l的方程为y=k(x-2)-1,
由$\left\{\begin{array}{l}{y=k(x-2)-1}\\{{x}^{2}=-4y}\end{array}\right.$,消去y得x2+4kx-8k-4=0,
∴△=(4k)2-4(-8k-4)=0,解得:k=-1,
∴直线l的方程是:x+y-1=0,
又∵直线l与圆c2相切,
∴d=$\frac{|m-1|}{\sqrt{2}}$=1,解得:m=$\sqrt{2}$+1,或m=1-$\sqrt{2}$(舍去),
∴c2的方程是x2+${[y-(\sqrt{2}+1)]}^{2}$=1;
(Ⅱ)设Q(x,y),则有$\left\{\begin{array}{l}{y=x+1}\\{\frac{y-(1+\sqrt{2})}{x}=1}\end{array}\right.$,解得:x=-$\frac{\sqrt{2}}{2}$,y=1+$\frac{\sqrt{2}}{2}$,
∴|PQ|=$\sqrt{{(2+\frac{\sqrt{2}}{2})}^{2}{+(-1-1-\frac{\sqrt{2}}{2})}^{2}}$=2$\sqrt{2}$+1,
设d为点N到直线PQ的距离,则S△NPQ=$\frac{|PQ|}{2}$d,
显然d的最大值为圆的直径,即点N与点Q位于直径的两端,
∴△NPQ面积的最大值为:S△NPQ=$\frac{|PQ|d}{2}$=$\frac{(1+2\sqrt{2})×2}{2}$=2$\sqrt{2}$+1.
点评 本题考察了求直线和曲线的方程问题,考察圆的切线问题,熟练掌握直线和圆的关系,两点间的距离,点到线的距离等基础知识是解答问题的根本,本题是一道中档题.

| A. | {x|2<x<3} | B. | {x|1<x<3} | C. | {x|1<x<4} | D. | {x|3<x<4} |
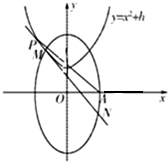 已知焦点在y轴上的椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)经过点Q($\frac{\sqrt{3}}{2}$,1),过椭圆的一个焦点且垂直长轴的弦长为1.
已知焦点在y轴上的椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)经过点Q($\frac{\sqrt{3}}{2}$,1),过椭圆的一个焦点且垂直长轴的弦长为1.