题目内容

8．已知函数f（x）是奇函数，且当x＞0时，f（x）=ex，则f（-1）=（　　）
A．$\frac{1}{e}$B．-$\frac{1}{e}$C．eD．-e

分析 直接利用函数的奇偶性以及函数的解析式求解即可．

解答 解：函数f（x）是奇函数，且当x＞0时，f（x）=ex，则f（-1）=-f（1）=-e．
故选：D．

点评 本题考查函数的奇偶性的应用，函数值的求法，考查计算能力．

练习册系列答案
相关题目
4．在数列{an}中，a1=3，an+1=$\frac{{3}^{n+1}{a}_{n}}{{a}_{n}+{3}^{n}}$
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=$\frac{1}{{a}_{n}}$，数列{bn}的前n项和为Tn，若a＞Tn对任意n∈N+恒成立，求实数a的取值范围．
19．已知圆O：x2+y2=2，过点A（1，1）的直线交圆O所得的弦长为$\frac{2\sqrt{5}}{5}$，且与x轴的交点为双曲线E：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1的右焦点F（c，0）（c＞2），双曲线E的离心率为$\frac{3}{2}$．
（1）求双曲线E的方程；
（2）过点P（$\frac{4}{3}$，5）作动直线l交双曲线右支于M、N两点，点Q异于M，N，且在线段MN上运动，并满足关系$\frac{|PM|}{|PN|}$=$\frac{|MQ|}{|ON|}$，试证明点Q恒在一条直线上．
16．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞1）过点P（-1，-1），c为椭圆的半焦距，且c=$\sqrt{2}$b．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过点P作两条相互垂直的直线l1，l2与椭圆C分别交于另两点M，N，若线段MN的中点在x轴上，求此时直线MN的方程．
3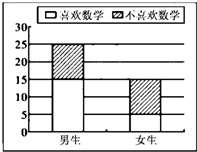．对某中学高二某班40名学生是否喜欢数学课程进行问卷调查，将调查所得数据绘制成二堆条形图如图所示．
（Ⅰ）根据图中相关数据完成以下2×2列联表；并计算在犯错误的概率不超过多少的前提下认为“性别与是否喜欢数学课程有关系”？
喜欢数学课程不喜欢数学课程总计
男
女
总计40
（Ⅱ）从该班所有女生中随机选取2人交流学习体会，求这2人中喜欢数学课程的人数X的分布列和数学期望．
参考公式：K2=$\frac{（a+b+c+d）（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
临界值附表：
P（K2≥k0）0.50.40.250.150.10.01
k00.4550.7081.3232.0722.7066.635
13．在△ABC中，内角A，B，C的对边分别是a，b，c，若$\frac{a}{b}=\frac{b+\sqrt{3}c}{a}$，sinC=2$\sqrt{3}$sinB，则tanA$\frac{\sqrt{3}}{3}$．
20．已知3≤2x+y≤9，且6≤x-y≤9，则z=x+2y的最小值为-6．
17．对于实数a，b，c中，给出下列命题：
①若a＞b，则ac2＞bc2    ②若ac2＞bc2，则a＞b   ③若a＜b＜0，则a2＞ab＞b2
④若a＜b＜0，则$\frac{1}{a}$＜$\frac{1}{b}$   ⑤若a＜b＜0，则$\frac{b}{a}$＞$\frac{a}{b}$   ⑥若a＜b＜0，则|a|＞|b|
⑦若c＞a＞b＞0，则$\frac{a}{c-a}$＞$\frac{b}{c-b}$                 ⑧若a＞b，$\frac{1}{a}$＞$\frac{1}{b}$，则a＞0，b＜0．
其中正确的命题是②③⑥⑧⑦．
18．如图，在矩形ABCD中，AB=2BC，E为线段AB的中点，将△ADE沿直线DE翻折成△A′DE，使平面A′DE⊥平面BCD，F为线段A′C的中点．
（Ⅰ）求证：A′D⊥平面A′EC；
（Ⅱ）设M为线段DE的中点，求直线FM与平面A′EC所成角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网