题目内容
2.若|x+a|-|x+1|<2a恒成立,求a的范围.分析 根据绝对值的性质求出|x+a|-|x+1|的最大值即可得到结论.
解答 解:由绝对值的性质可知,
若a>1,则|x+a|-|x+1|≤-1-(-a)=a-1,
此时由a-1<2a得a>-1,此时a>1,
若a≤1,则|x+a|-|x+1|≤1-a,
此时由a-1<2a得a>-1,此时-1<a≤1,
综上a>-1,
即a的范围是(-1,+∞).
点评 本题主要考查不等式恒成立问题,根据绝对值不等式的性质是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设集合A={x|x2-6x+8<0},B={x|2<2x<8},则A∪B=( )
| A. | {x|2<x<3} | B. | {x|1<x<3} | C. | {x|1<x<4} | D. | {x|3<x<4} |
11.已知等差数列{an}的前三项为a-1,4,2a,记前n项和为Sn,设bn=$\frac{{S}_{n}}{n}$,则b3+b7+b11+…+b4n-1等于( )
| A. | n2+n | B. | 2n2+2n | C. | n2-n | D. | 2n2-2n |
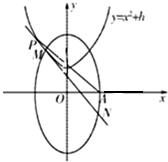 已知焦点在y轴上的椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)经过点Q($\frac{\sqrt{3}}{2}$,1),过椭圆的一个焦点且垂直长轴的弦长为1.
已知焦点在y轴上的椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)经过点Q($\frac{\sqrt{3}}{2}$,1),过椭圆的一个焦点且垂直长轴的弦长为1.