题目内容
5.已知函数f(x)=$\frac{3x}{2x+1}$,数列{an}满足:a1=$\frac{3}{2}$,且an=f(an-1)(n∈N*,n≥2)(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明:a1a2a3…an<2.
分析 (Ⅰ)由已知结合数列的函数特性得到数列递推式,进一步构造出等比数列数列{$\frac{1}{{a}_{n}}-1$},求其通项公式后可得数列{an}的通项公式;
(Ⅱ)把证明a1a2a3…an<2转化为证明a1a2a3…an<$2•\frac{{3}^{n}-1}{{3}^{n}}$,然后利用数学归纳法证明.
解答 (Ⅰ)解:由f(x)=$\frac{3x}{2x+1}$,an=f(an-1),得${a}_{n}=\frac{3{a}_{n-1}}{2{a}_{n-1}+1}(n≥2)$,
即$\frac{1}{{a}_{n}}=\frac{1}{3}•\frac{1}{{a}_{n-1}}+\frac{2}{3}$,∴$\frac{1}{{a}_{n}}-1=\frac{1}{3}(\frac{1}{{a}_{n-1}}-1)$(n≥2),
∵a1=$\frac{3}{2}$,$\frac{1}{{a}_{1}}-1=\frac{2}{3}-1=-\frac{1}{3}$.
∴数列{$\frac{1}{{a}_{n}}-1$}是以-$\frac{1}{3}$为首项,以$\frac{1}{3}$为公比的等比数列,
则$\frac{1}{{a}_{n}}-1=-\frac{1}{3}•(\frac{1}{3})^{n-1}=-(\frac{1}{3})^{n}$,
∴${a}_{n}=\frac{{3}^{n}}{{3}^{n}-1}$;
(Ⅱ)证明:当n=2时,a1a2 =$\frac{3}{2}×\frac{9}{8}=\frac{27}{16}$<$\frac{16}{9}$=2$•\frac{9-1}{9}$<2.
假设当n=k(k≥2)时,a1a2…ak <2$•\frac{{3}^{k}-1}{{3}^{k}}$<2,
那么,当n=k+1时,a1a2…ak ak+1<2•$\frac{{3}^{k}-1}{{3}^{k}}$$•\frac{{3}^{k+1}}{{3}^{k+1}-1}$.
要证明2•$\frac{{3}^{k}-1}{{3}^{k}}$$•\frac{{3}^{k+1}}{{3}^{k+1}-1}$<$2•\frac{{3}^{k+1}-1}{{3}^{k+1}}$,
只需证明 3k+1•3k+1 ( 3k-1)<3k•(3k+1-1)2,
只要证 3×3k+1( 3k-1)<(3k+1-1)2,32k+2-3k+2<32k+2-2•3k+1+1,
3k+2>2•3k+1-1,3k+1>-1.
而3k+1>-1 显然成立,∴n=k+1 时,a1a2…ak ak+1<2$•\frac{{3}^{k+1}-1}{{3}^{k+1}}$<2,
综上得a1a2…ak ak+1<2•$\frac{{3}^{k+1}-1}{{3}^{k+1}}$<2.
又当n=1时,a1=$\frac{3}{2}$<2,
∴a1a2a3…an<$2•\frac{{3}^{n}-1}{{3}^{n}}$<2.
点评 本题考查了数列递推式,考查了等比数列的构造和通项公式的求法,训练了利用数学归纳法证明数列不等式,属难度较大的题目.

 同步奥数系列答案
同步奥数系列答案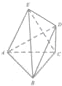 已知AC=BC=$\sqrt{2}$,CD=$\frac{\sqrt{3}}{2}$,AB=BE=EA=2,CD⊥面ABC,面ABE⊥面ABC.
已知AC=BC=$\sqrt{2}$,CD=$\frac{\sqrt{3}}{2}$,AB=BE=EA=2,CD⊥面ABC,面ABE⊥面ABC. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)一个顶点为A(0,1),直线l:y=-x+2恰好与椭圆相切.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)一个顶点为A(0,1),直线l:y=-x+2恰好与椭圆相切.