题目内容
6.盒中装有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量,求X的分布列.分析 从盒中任取3个,这3个可能全是旧的,2个旧的1个新的,1个旧的2个新的或全是新的,所以用完放回盒中,盒中旧球个数可能是3个,4个,5个,6个,即X可以取3,4,5,6.X取每个值的概率可由古典概型求得,列出分布列即可.
解答 解:X的所有可能取值为3,4,5,6.
P(X=3)=$\frac{{C}_{3}^{3}}{{C}_{12}^{3}}=\frac{1}{220}$
P(X=4)=$\frac{{C}_{9}^{1}{C}_{3}^{2}}{{C}_{12}^{3}}=\frac{27}{220}$P(X=5)=$\frac{{C}_{9}^{2}{C}_{3}^{1}}{{C}_{12}^{3}}=\frac{27}{55}$,P(X=6)=$\frac{{C}_{9}^{3}}{{C}_{12}^{3}}=\frac{21}{55}$
所以X的分布列为
| X | 3 | 4 | 5 | 6 |
| P | $\frac{1}{220}$ | $\frac{27}{220}$ | $\frac{27}{55}$ | $\frac{21}{55}$ |
点评 本题考查排列组合、古典概型、离散型随机变量的分布列问题,解题的关键是正确地求出X取某个值时对应的事件的概率.

练习册系列答案
相关题目
1.四棱锥S-ABCD中,底面ABCD是边长为2$\sqrt{3}$的正方形,SA⊥平面ABCD,且SA=2$\sqrt{6}$,则此四棱锥的外接球的表面积为( )
| A. | 12π | B. | 24π | C. | 144π | D. | 48π |
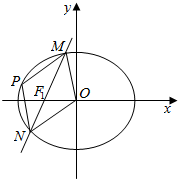 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$,且$a=\sqrt{2}b$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$,且$a=\sqrt{2}b$.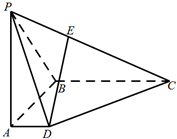 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为6.
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为6.