题目内容
11.等边三角形ABC的顶点A,B在圆O:x2+y2=1上,则|OC|的最大值为2.分析 根据题意画出图形,利用圆与等边三角形的对称性得出|OC|取最大值时,OC过AB的中点M,
设|AB|=x,表示出|OC|的大小,借助于导数求出|OC|的最大值.
解答 解:等边三角形ABC的顶点A,B在圆O:x2+y2=1上,如图所示;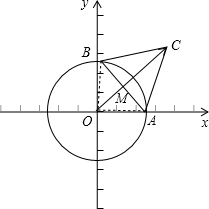 ⊥
⊥
根据圆与等边三角形的对称性知,
当|OC|取最大值时,OC过AB的中点M,
设|AB|=x,则|CM|=$\frac{\sqrt{3}}{2}$x,
|OM|=$\sqrt{{1}^{2}{-(\frac{x}{2})}^{2}}$=$\frac{1}{2}$$\sqrt{4{-x}^{2}}$,
∴|OC|=|OM|+|CM|
=$\frac{1}{2}$$\sqrt{4{-x}^{2}}$+$\frac{\sqrt{3}}{2}$x
=$\frac{1}{2}$($\sqrt{4{-x}^{2}}$+$\sqrt{3}$x),0<x≤2;
设y=$\sqrt{4{-x}^{2}}$+$\sqrt{3}$x,(0<x≤2),
∴y′=$\frac{1}{2}$•$\frac{1}{\sqrt{4{-x}^{2}}}$•(-2x)+$\sqrt{3}$=$\frac{-x+\sqrt{3}•\sqrt{4{-x}^{2}}}{\sqrt{4{-x}^{2}}}$,
令y′=0,得-x+$\sqrt{3}$•$\sqrt{4{-x}^{2}}$=0,
解得x=±$\sqrt{3}$,应取x=$\sqrt{3}$;
当x∈(0,$\sqrt{3}$)时,y′>0,y是增函数,
当x∈($\sqrt{3}$,2]时,y′<0,y是减函数,
∴当x=$\sqrt{3}$时,y取得最大值为
ymax=$\sqrt{4{-(\sqrt{3})}^{2}}$+$\sqrt{3}$×$\sqrt{3}$=4,
∴|OC|的最大值为2.
故答案为:2.
点评 本题考查了直线与圆的方程的应用问题,也考查了数形结合的应用问题,考查了利用导数求函数最值的应用问题,是综合性题目.

| A. | 36种 | B. | 39种 | C. | 60种 | D. | 78种 |
| A. | 24 | B. | 25 | C. | 26 | D. | 27 |
| A. | (-∞,0)∪($\frac{1}{2}$,+∞) | B. | [0,$\frac{1}{2}$] | C. | (0,$\frac{1}{2}$ ) | D. | (-∞,0]∪[$\frac{1}{2}$,+∞) |
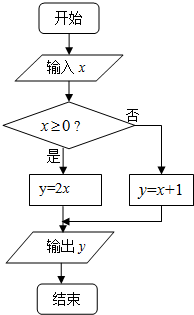
| A. | 3 | B. | 0 | C. | -4 | D. | -5 |
 如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且$\frac{AP}{PC}$=$\frac{AQ}{QO}$=2.
如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且$\frac{AP}{PC}$=$\frac{AQ}{QO}$=2.