题目内容

18．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为6．

分析 根据三视图得出该几何体是在棱长为4的正方体中的三棱锥，画出图形，得出最长的棱长是哪一条，求出值即可．

解答 解：根据题意，得；
该几何体是如图所示的三棱锥A-BCD，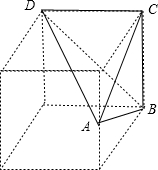
且该三棱锥是放在棱长为4的正方体中，
所以，在三棱锥A-BCD中，最长的棱长为AD，
且AD=$\sqrt{{CD}^{2}{+AC}^{2}}$=$\sqrt{{4}^{2}+{（4}^{2}{+2}^{2}）}$=6．
故答案为：6．

点评 本题考查了空间几何体三视图的应用问题，解题的关键是由三视图还原为几何体，是基础题．

练习册系列答案
相关题目
8．已知m∈R，n∈R，并且m+3n=1，则em+e3n的最小值$2\sqrt{e}$．
9．已知函数f（x）=cos（$\frac{aπ}{3}$x），a为抛掷一颗骰子所得的点数，则函数f（x）在[0，4]上零点的个数小于5或大于6的概率为（　　）
A．$\frac{2}{3}$B．$\frac{5}{6}$C．$\frac{2}{5}$D．$\frac{1}{3}$
6．盒中装有12个乒乓球，其中9个新的，3个旧的，从盒中任取3个来用，用完后装回盒中，此时盒中旧球个数X是一个随机变量，求X的分布列．
13．复数z满足i•z=1+i，其中i为虚数单位，则在复平面上复数z对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
3．已知函数f（x）=ex（asinx+bcosx）在（0，1）处的切线与直线y=2x+e平行．
（1）求a，b的值及函数f（x）的单调区间；
（2）当0＜x＜1时，求证：f（x）＞（1+x-x2）ln（x+2）
10．已知矩阵A=$[\begin{array}{l}{a}&{b}\\{2}&{1}\end{array}]$，若矩阵A属于特征值-1的一个特征向量为α1=$[\begin{array}{l}{1}\\{-1}\end{array}]$，属于特征值4的一个特征向量为α2=$[\begin{array}{l}{3}\\{2}\end{array}]$．求矩阵A，并写出A的逆矩阵A-1．
7．已知f（x）=$\left\{\begin{array}{l}{lnx，x＞0}\\{-ln（-x），x＜0}\end{array}\right.$，若f（a）＞f（-a），则实数a的取值范围是（-1，0）∪（1，+∞）．
8．i是虚数单位，复数$\frac{2-2i}{1+i}$=（　　）
A．2B．-2C．2iD．-2i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网