Question

【题目】已知椭圆方程为 +y2=1，圆C：（x﹣1）2+y2=r2 ．
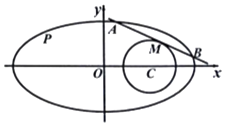
（Ⅰ）求椭圆上动点P与圆心C距离的最小值；
（Ⅱ）如图，直线l与椭圆相交于A、B两点，且与圆C相切于点M，若满足M为线段AB中点的直线l有4条，求半径r的取值范围．

Answer 1

【答案】解：（Ⅰ）设P（x，y），丨PC丨= = = ，

由﹣2≤x≤2，当x= 时，丨PC丨min= ，

（Ⅱ）当直线AB斜率不存在时且与椭圆C相切时，M在x轴上，

故满足条件的直线有两条；

当直线AB斜率存在时，设A（x1，y1），B（x2，y2），M（x0，y0），

由 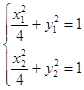，整理得： =﹣ × ，

则kAB=﹣ ，kMC= ，kMC×kAB=﹣1，

则kMC×kAB=﹣ × =﹣1，解得：x0= ，

由M在椭圆内部，则 ，解得：y02＜ ，

由：r2=（x0﹣1）2+y02= +y02，

∴ ＜r2＜ ，解得： ＜r＜ ．

∴半径r的取值范围（ ， ）

【解析】（Ⅰ）利用两点之间的距离公式，根据x的取值范围，即可求得丨PC丨的最小值；（Ⅱ）利用点差法求得直线AB的斜率，根据kMC×kAB=﹣1，求得M点坐标，由 ，求得y02＜ ，由圆的方程，即可求得半径r的取值范围．