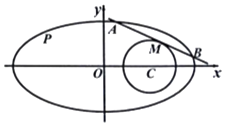
题目内容
【题目】已知向量 
， 
满足| |=3，| |=2| 
|，若| +λ |≥3恒成立，则实数λ的取值范围为 ．
【答案】（﹣∞,﹣ 
）∪[ 
,+∞）
【解析】解：设 
， 
= 
，则 
= 
，
设| 
|=x，则|OA|=x，|AB|= 
，
∴ 
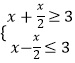，解得2≤x≤6．
即2≤| |≤6．
∵| |=2| |，
∴ 
=4（9﹣2 
+ 2），即3 ﹣8 +36=0，
∴ = 
+ 
，
∵| +λ |≥3恒成立，
∴ +2λ（ + ）+9λ2≥9，
令f（ 2）=（1+ 
λ） 2+9λ+9λ2﹣9，则fmin（ ）≥0， ∈[4，36]．
（i）若1+ λ=0即λ=﹣ 
时，f（ ）=9λ+9λ2﹣9=﹣5，不符合题意；
（ii）若1+ 
＞0即λ＞﹣ 时，f（ ）为增函数，故fmin（ ）=f（4）=9λ2+12λ﹣5≥0，
解得λ 
或λ≤﹣ 
，∴λ≥ 
．
（iii）若1+ ＜0即λ＜﹣ 时，f（ ）为减函数，故fmin（ ）=f（36）=9λ2+36λ+27≥0，
解得λ≤1或λ≥3．∴λ＜﹣ ．
综上，λ＜﹣ 或λ ．
所以答案是：（﹣∞，﹣ ）∪[ ，+∞）．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某汽车的使用年数x与所支出的维修费用y的统计数据如表：
使用年数x（单位：年） | 1 | 2 | 3 | 4 | 5 |
维修总费用y（单位：万元） | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
根据上表可得y关于x的线性回归方程 
= 
x﹣0.69，若该汽车维修总费用超过10万元就不再维修，直接报废，据此模型预测该汽车最多可使用（ ）
A.8年
B.9年
C.10年
D.11年
