Question

【题目】已知椭圆C： （a＞b＞0）过点（ ，1），且焦距为2 ．
（1）求椭圆C的方程；
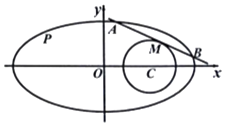
（2）若直线l：y=k（x+1）（k＞﹣2）与椭圆C相交于不同的两点A、B，线段AB的中点M到直线2x+y+t=0的距离为 ，求t（t＞2）的取值范围．

Answer 1

【答案】
（1）解：由2c=2 ，c= ，则a2﹣b2=2，

将点（ ，1）代入椭圆方程： ，解得：a2=4，b2=2，

∴椭圆的标准方程：

（2）解：A（x1，y1），B（x2，y2），M（x0，y0）

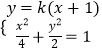，整理得：（2k2+1）x2+4k2x+2k2﹣4=0，

则x1+x2=﹣ ，则x0= =﹣ ，

y0=k（x0+1）= ，

由M到直线2x+y+t=0的距离 ， = ，

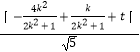则丨 +t﹣2丨=3，

由k＞﹣2及t＞2，则t=5﹣ =5﹣ ，

由 ≥6 ，

∴5﹣ ≤t＜5，即4﹣ ≤t＜5，

∴t（t＞2）的取值范围[4﹣ ，5）

【解析】（1）由c= ，则a2﹣b2=2，将点代入椭圆方程，联立即可求得a和b的值，即可求得椭圆方程；（2）将直线方程代入椭圆方程，利用韦达定理及中点坐标公式求得M点坐标，利用点到直线的距离公式，根据k及t的取值范围，利用基本不等式的性质，即可求得t的取值范围．