题目内容
【题目】已知函数f(x)=x2+ax+b(a、b∈R)在区间[0,1]上有零点,则ab的最大值是 .
【答案】![]()
【解析】解:∵函数f(x)=x2+ax+b(a、b∈R)在区间[0,1]上有零点,
∴△=a2﹣4b≥0,
(i)若△=0,即b= ![]() 时,f(x)的零点为x=﹣
时,f(x)的零点为x=﹣ ![]() ,
,
∴0≤﹣ ![]() ≤1,即﹣2≤a≤0,
≤1,即﹣2≤a≤0,
∴ab= ![]() ,
,
∴当a=0时,ab取得最大值0;
(ii)若△>0,即b< ![]() ,
,
①若函数f(x)=x2+ax+b(a、b∈R)在区间[0,1]上有一个零点,则f(0)f(1)≤0,
∴b(1+a+b)≤0,
即b+b2+ab≤0,
∴ab≤﹣b2﹣b=﹣(b+ ![]() )2+
)2+ ![]() ,
,
∴ab的最大值是 ![]() ;
;
②若函数f(x)=x2+ax+b(a、b∈R)在区间[0,1]上有两个零点,
∴ 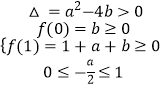 ,即
,即 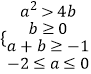
显然ab≤0,
综上,ab的最大值为 ![]() .
.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目