题目内容
【题目】设函数f（x）=|2x﹣1|+|2x﹣3|，x∈R．
（1）解不等式f（x）≤5；
（2）若f（x）+m≠0恒成立，求实数m的取值范围．
【答案】
（1）解：问题等价于 
或 
或 
，
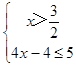故不等式的解集是[﹣ 
， 
]
（2）解：若f（x）+m≠0恒成立，
即f（x）+m=0在R上无解，
又f（x）=|2x﹣1|+|2x﹣3|≥|2x﹣1﹣2x+3|=2，
故f（x）的最小值是2，
故m＞﹣2
【解析】（1）通过讨论x的范围，求出不等式的解集即可；（2）根据绝对值的性质求出f（x）的最小值，从而求出m的范围即可．
【考点精析】利用绝对值不等式的解法对题目进行判断即可得到答案，需要熟知含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．
练习册系列答案
相关题目
【题目】某汽车的使用年数x与所支出的维修费用y的统计数据如表：
使用年数x（单位：年） | 1 | 2 | 3 | 4 | 5 |
维修总费用y（单位：万元） | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
根据上表可得y关于x的线性回归方程 
= 
x﹣0.69，若该汽车维修总费用超过10万元就不再维修，直接报废，据此模型预测该汽车最多可使用（ ）
A.8年
B.9年
C.10年
D.11年
