题目内容
【题目】已知函数
设
表示p、q中的较大值，
表示p、q中的较小值）记
的最小值为A，
的最大值为B，则A-B＝
A. 16 B. -16 C. a2-2a-16 D. a2+2a-1
【答案】B
【解析】
在同一坐标系中画出f（x）与g（x）的图象，由图象及H1（x）的定义知H1（x）的最小值是f（a+2），H2（x）的最大值为g（a﹣2），进而可得答案．
f（x）＝g（x），
即x2﹣2（a+2）x+a2＝﹣x2+2（a﹣2）x﹣a2+8，
即x2﹣2ax+a2﹣4＝0，
解得x＝a+2或x＝a﹣2．
f（x）与g（x）的图象如图．
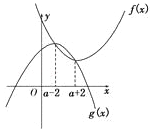
由图象及H1（x）的定义知H1（x）的最小值是f（a+2），
H2（x）的最大值为g（a﹣2），
A﹣B＝f（a+2）﹣g（a﹣2）
＝（a+2）2﹣2（a+2）2+a2+（a﹣2）2﹣2（a﹣2）2+a2﹣8＝﹣16．
故答案为：B
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
【题目】某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，现用一种新配方做试验，生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：
质量指标值 |
|
|
|
|
|
频数 | 6 | 26 | 38 | 22 | 8 |
（1）将答题卡上列出的这些数据的频率分布表填写完整，并补齐频率分布直方图；
（2）估计这种产品质量指标值的平均值（同一组中的数据用该组区间的中点值作代表）与中位数（结果精确到0.1）.
质量指标值分组 | 频数 | 频率 |
| 6 | 0.06 |
| ||
| ||
| ||
| ||
合计 | 100 | 1 |
