题目内容
【题目】已知向量![]() ,
,![]() ,函数
,函数![]() 满足
满足![]() ,且在区间
,且在区间![]() 上单调,又不等式
上单调,又不等式![]() 对一切
对一切![]() 恒成立.
恒成立.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 的零点为
的零点为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据![]() 利用向量数量积公式与正弦的和角公式化简,再根据题意可得
利用向量数量积公式与正弦的和角公式化简,再根据题意可得![]() 的对称轴与对称中心等.同时利用
的对称轴与对称中心等.同时利用![]() 在区间
在区间![]() 上单调求出关于周期的不等式,继而求得解析式.
上单调求出关于周期的不等式,继而求得解析式.
(2)将题意转换为函数![]() 的图象与
的图象与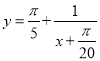 的图象在区间
的图象在区间![]() 上有100个交点.再利用函数的对称点分析求解即可.
上有100个交点.再利用函数的对称点分析求解即可.
(1)![]()
因为![]() ,所以
,所以![]() 是函数
是函数![]() 的一个对称中心,
的一个对称中心,
由![]() ,得
,得![]() 为函数
为函数![]() 的一条对称轴,
的一条对称轴,
所以![]() ,即
,即![]()
所以![]() .
.
又因为函数![]() 在区间
在区间![]() 上单调,所以
上单调,所以![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() .
.
又因为![]() 所以
所以![]() 又
又![]() 所以
所以![]() .
.
所以![]() .
.
(2)由题意,方程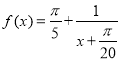 在区间
在区间![]() 上有100个实根,
上有100个实根,
即函数![]() 的图象与
的图象与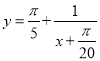 的图象在区间
的图象在区间![]() 上有100个交点.
上有100个交点.
由![]() 得
得![]() ,
,
所以![]() 为函数
为函数![]() 的图象的一个对称中心.
的图象的一个对称中心.
易知![]() 也是函数
也是函数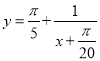 的图象的对称中心,
的图象的对称中心,
所以![]() 与
与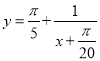 的图象交点成对出现,且每一对均关于点
的图象交点成对出现,且每一对均关于点![]() 对称,
对称,
所以![]() .
. ![]() ,
,
所以![]() =
=![]() .
.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
【题目】通过随机询问72名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
男 | 女 | 总计 | ||
读营养说明 | 16 | 28 | 44 | |
不读营养说明 | 20 | 8 | 28 | |
总计 | 36 | 36 | 72 |
(1)根据以上列联表判断,能否在犯错误的概率不超过0.005的前提下认为性别和是否看营养说明有关系呢?
(2)从被询问的28名不读营养说明的大学生中,随机抽取2名学生,求抽到女生人数![]()
的分布列及数学期望.
附:
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
![]()
