题目内容
【题目】（选修4-4：坐标系与参数方程）
在直角坐标系
中，半圆C的参数方程为
（
为参数，
），以O为极点，x轴的非负半轴为极轴建立极坐标系.
（Ⅰ）求C的极坐标方程；
（Ⅱ）直线
的极坐标方程是
，射线OM：
与半圆C的交点为O、P，与直线的交点为Q，求线段PQ的长.
【答案】（1）
；（2）4.
【解析】
试题本题主要考查极坐标方程与直角坐标方程的转化、参数方程与普通方程的转化等基础知识，意在考查考生的分析问题解决问题的能力、转化能力、运算求解能力.第一问，先利用参数方程与普通方程的转化公式将圆C的方程转化为普通方程，再利用公式
转化为极坐标方程；第二问，利用圆C的极坐标方程求出点P的极坐标，再利用直线
的极坐标方程求出点Q的极坐标，最后利用
计算即可.
试题解析：（Ⅰ）半圆C的普通方程为
，又，
所以半圆C的极坐标方程是． （5分）
（Ⅱ）设
为点P的极坐标，则有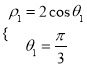
，解得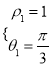
，
设
为点Q的极坐标，则有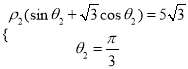
解得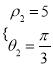
，
由于
，所以
，所以PQ的长为4． （10分）
练习册系列答案
期末集结号系列答案
相关题目
【题目】某公司培训员工某项技能，培训有如下两种方式：
方式一：周一到周五每天培训1小时，周日测试
方式二：周六一天培训4小时，周日测试
公司有多个班组，每个班组60人，现任选两组
记为甲组、乙组
先培训；甲组选方式一，乙组选方式二，并记录每周培训后测试达标的人数如表：
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
用方式一与方式二进行培训，分别估计员工受训的平均时间精确到
，并据此判断哪种培训方式效率更高？
在甲乙两组中，从第三周培训后达标的员工中采用分层抽样的方法抽取6人，再从这6人中随机抽取2人，求这2人中至少有1人来自甲组的概率．
