题目内容
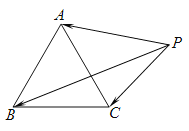
【题目】如图,![]() 是边长为1的正三角形,点P在
是边长为1的正三角形,点P在![]() 所在的平面内,且
所在的平面内,且![]() (a为常数),下列结论中正确的是( )
(a为常数),下列结论中正确的是( )
A.当![]() 时,满足条件的点P有且只有一个
时,满足条件的点P有且只有一个
B.当![]() 时,满足条件的点P有三个
时,满足条件的点P有三个
C.当![]() 时,满足条件的点P有无数个
时,满足条件的点P有无数个
D.当a为任意正实数时,满足条件的点总是有限个
【答案】C
【解析】
以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 中点为原点,建立直角坐标系,如图所示设
中点为原点,建立直角坐标系,如图所示设![]() ,将式子
,将式子![]() 化为关于
化为关于![]() 、
、![]() 、
、![]() 的式子,化简整理可得
的式子,化简整理可得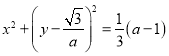 ,讨论
,讨论![]() 的取值范围,可得当
的取值范围,可得当![]() 时方程表示以点
时方程表示以点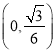 为圆心,半径
为圆心,半径![]() 的圆,满足条件的点
的圆,满足条件的点![]() 有无数个,可知只有
有无数个,可知只有![]() 项符合题意.
项符合题意.
以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 中点为原点,建立直角坐标系,如图所示
中点为原点,建立直角坐标系,如图所示
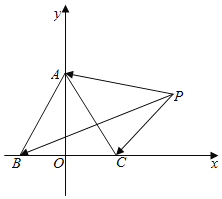
则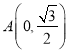 ,
,![]() ,
,![]() ,
,
设![]() ,可得
,可得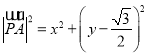 ,
,
![]() ,
,![]() ,
,
∵![]() ,
,
∴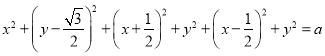 ,
,
化简得:![]() ,即
,即![]() ,
,
配方,得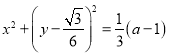 …(1)
…(1)
当![]() 时,方程(1)的右边小于0,故不能表示任何图形;
时,方程(1)的右边小于0,故不能表示任何图形;
当![]() 时,方程(1)的右边为0,表示点
时,方程(1)的右边为0,表示点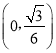 ,恰好是正三角形的重心;
,恰好是正三角形的重心;
当![]() 时,方程(1)的右边大于0,表示以
时,方程(1)的右边大于0,表示以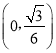 为圆心,半径为
为圆心,半径为![]() 的圆,
的圆,
由此对照各个选项,可得只有C项符合题意.
故选:C.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目