题目内容
【题目】已知点![]() 和椭圆
和椭圆![]() .直线
.直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() 的面积;
的面积;
(2)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,当
,当![]() 为
为![]() 中点时,求
中点时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)联立直线![]() 的方程和椭圆方程,求得交点的横坐标,由此求得三角形
的方程和椭圆方程,求得交点的横坐标,由此求得三角形![]() 的面积.
的面积.
(2)法一:根据![]() 的坐标求得
的坐标求得![]() 的坐标,将
的坐标,将![]() 的坐标都代入椭圆方程,化简后求得
的坐标都代入椭圆方程,化简后求得![]() 的坐标,进而求得
的坐标,进而求得![]() 的值.
的值.
法二:设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和椭圆的方程,化简后写出根与系数关系,结合
的方程和椭圆的方程,化简后写出根与系数关系,结合![]() 求得
求得![]() 点的坐标,进而求得
点的坐标,进而求得![]() 的值.
的值.
(1)设![]() ,
,![]() ,
,
若![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
由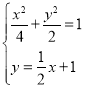 ,得
,得![]() ,
,
解得![]() ,
,![]() ,
,
设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]() 且
且
![]() .
.
(2)法一:设点![]()
因为![]() ,
,![]() ,所以
,所以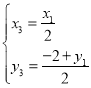
又点![]() ,
,![]() 都在椭圆上,
都在椭圆上,
所以
解得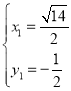 或
或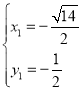
所以![]() 或
或![]() .
.
法二:设![]()
显然直线![]() 有斜率,设直线
有斜率,设直线![]() 的方程为
的方程为![]()
由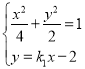 ,得
,得![]()
所以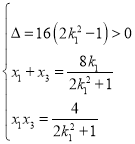
又![]()
解得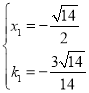 或
或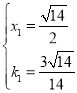
所以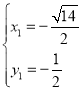 或
或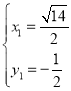
所以![]() 或
或![]() .
.

 互动英语系列答案
互动英语系列答案【题目】每个国家对退休年龄都有不一样的规定,从2018年开始我国关于延迟退休的话题一直在网上热议,为了了解市民对“延迟退休”的态度,现从某地市民中随机选取100人进行调查,调查情况如下表:
年龄段(单位:岁) |
|
|
|
|
|
|
被调查的人数 |
|
|
|
|
|
|
赞成的人数 |
|
|
|
|
|
|
(1)从赞成“延迟退休”的人中任选1人,此人年龄在![]() 的概率为
的概率为![]() ,求出表格中
,求出表格中![]() 的值;
的值;
(2)在被调查的人中,年龄低于35岁的人可以认为“低龄人”,年龄不低于35岁的人可以认为“非低龄人”,试作出是否赞成“延迟退休”与“低龄与否”的![]() 列联表,并指出有无
列联表,并指出有无![]() 的把握认为是否赞成“延迟退休”与“低龄与否”有关,并说明理由.
的把握认为是否赞成“延迟退休”与“低龄与否”有关,并说明理由.
附:![]() .
.
|
|
|
|
|
|
|
|
|
|
【题目】随着共享单车的成功运营,更多的共享产品逐步走人大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷,某公司随机抽取1000人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的1000人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)求出表格中![]() 的值,并根据表中的数据,判断能否在犯错误的概率不超过
的值,并根据表中的数据,判断能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品对生活无益的人员中随机抽取6人,再从6人中随机抽取2人赠送超市购物券作为答谢,求恰有1人是女性的概率.
参考公式: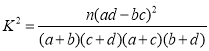 .
.
|
|
|
|
|
|
|
|
|
|
【题目】大荔县某高中一社团为调查学生学习围棋的情况,随机抽取了![]() 名学生进行调查.根据调查结果绘制的学生均学习围棋时间的频率分布直方图.将日均学习围棋时不低于
名学生进行调查.根据调查结果绘制的学生均学习围棋时间的频率分布直方图.将日均学习围棋时不低于![]() 分钟的学生称为“围棋迷”.
分钟的学生称为“围棋迷”.
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 |
|
| |
合计 |

(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
(2)现在从参与本次抽样调查的![]() 名学生的男同学里面,依据是否为围棋迷,采用分层抽样的方法抽取
名学生的男同学里面,依据是否为围棋迷,采用分层抽样的方法抽取![]() 名学生参与围棋知识竞赛,再从
名学生参与围棋知识竞赛,再从![]() 人中任选
人中任选![]() 人参与知识竞赛的赛前保障工作.求选到的
人参与知识竞赛的赛前保障工作.求选到的![]() 人恰好是一个“围棋迷”和一个“非围棋迷”的概率?
人恰好是一个“围棋迷”和一个“非围棋迷”的概率?
附:![]() ,
,
|
|
|
|
|
|
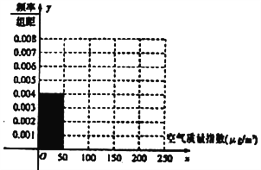
【题目】全世界越来越关注环境保护问题,某监测站点于2018年1月某日起连续![]() 天监测空气质量指数(
天监测空气质量指数(![]() ),数据统计如下:
),数据统计如下:
空气质量指数( |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
(1)根据所给统计表和频率分布直方图中的信息求出![]() ,
,![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的众数和中位数;
(3)在空气质量指数分别属于![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,再从中任意选取
天,再从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.