Question

【题目】全世界越来越关注环境保护问题，某监测站点于2018年1月某日起连续天监测空气质量指数()，数据统计如下：

空气质量指数()
空气质量等级	空气优	空气良	轻度污染	中度污染	重度污染
天数	20	40		10	5

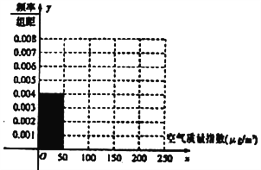
（1）根据所给统计表和频率分布直方图中的信息求出，的值，并完成频率分布直方图；

（2）由频率分布直方图，求该组数据的众数和中位数；

（3）在空气质量指数分别属于和的监测数据中，用分层抽样的方法抽取天，再从中任意选取天，求事件“两天空气都为良”发生的概率.

Answer 1

【答案】(1)答案见解析；(2)答案见解析；(3).

【解析】分析：（1）利用统计表和频率分布直方图能求出n，m的值，并能完成频率分布直方图；

（2）由频率分布直方图能求出该组数据的平均数和中位数；

（3）气质量指数为和的监测天数中分别抽取4天和1天，在所抽取的5天中，将空气质量指数为的天分别记为，，，；将空气质量指数为的天记为，从中任取天，利用列举法能求出事件“两天空气都为良”发生的概率.

解析：（1）∵，∴，∵，∴，

；；；.

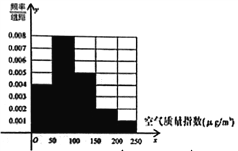
（2）众数为120.中位数为.

（3）在空气质量指数为和的监测天数中分别抽取天和天，在所抽取的天中，将空气质量指数为的天分别记为，，，；将空气质量指数为的天记为，从中任取天的基本事件分别为：，，，，，，，，，共种，其中事件“两天空气都为良”包含的基本事件为，，，，，共种，所以事件“两天都为良”发生的概率是.