题目内容
10.设函数f(x)=(sinx+cosx)2+2cos2x.(1)求函数f(x)的最小正周期;
(2)求f(x)在区间$[{0,\;\frac{π}{6}}]$上的最大值和最小值.
分析 (1)由条件化简函数的解析式,再根据正弦函数的周期性求得f(x)的最小正周期.
(2)由条件利用正弦函数的定义域和值域求得f(x)在区间$[{0,\;\frac{π}{6}}]$上的最大值和最小值.
解答 解:(1)由于函数f(x)=(sinx+cosx)2+2cos2x=1+sin2x+cos2x+1=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+2,
所以函数f(x)的最小正周期为$\frac{2π}{2}$=π.
(2)由$0≤x≤\frac{π}{6}$得:$\frac{π}{4}≤2x+\frac{π}{4}≤\frac{7π}{12}$,
当$2x+\frac{π}{4}=\frac{π}{4}$即x=0时,f(x)min=3;
当$2x+\frac{π}{4}=\frac{π}{2}$即$x=\frac{π}{8}$时,$f{(x)_{max}}=\sqrt{2}+2$.
点评 本题主要考查三角恒等变换、正弦函数的周期性、定义域和值域,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
1.一只小狗在如图所示的方砖上走来走去,求最终停在阴影方砖上的概率为( )
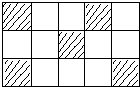

| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
 一个圆分成6个大小不等的小扇形,取来红、黄、蓝、白、绿、黑6种颜色,如图.
一个圆分成6个大小不等的小扇形,取来红、黄、蓝、白、绿、黑6种颜色,如图.