题目内容
15．
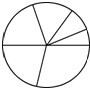一个圆分成6个大小不等的小扇形，取来红、黄、蓝、白、绿、黑6种颜色，如图．（1）6个小扇形分别着上6种颜色，有多少种不同的方法？
（2）从这6种颜色中任选5种着色，但相邻两个扇形不能着相同的颜色，有多少种不同的方法？
分析 （1）6个小扇形分别着上6种颜色，全排列即可，
（2）利用间接法，6个扇形从6种颜色中任选5种着色，再排除其中相邻两个扇形是同一种颜色的着色方法，问题得以解决．
解答 解：（1）6个小扇形分别着上6种不同的颜色，共有A66=720种着色方法．
（2）6个扇形从6种颜色中任选5种着色共有C62C65A55不同的方法，其中相邻两个扇形是同一种颜色的着色方法共有6C65A55此满足条件的着色方法共有
C62C65A55-6C65A55=6480种着色方法．
点评 本题考了排列组合种的染色问题，采用间接法是常用的方法，属于中档题．
练习册系列答案
相关题目
5．一个算法的程序框图如图所示，若运行该程序后输出的结果为$\frac{4}{5}$，则判断框中应填入的条件是（ ）
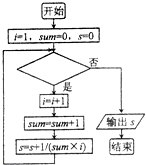
| A． | i≤5？ | B． | i≤4？ | C． | i≥4？ | D． | i≥5？ |
6．设a＞0，b＞0，若$\sqrt{3}$是93a与3b的等比中项，则$\frac{2}{a}+\frac{1}{b}$的最小值为（ ）
| A． | 1 | B． | 13+$4\sqrt{3}$ | C． | 2$\sqrt{3}$ | D． | $\frac{13}{2}+2\sqrt{3}$ |
20．已知函数f（x）=ex+x2-x，若对任意x1，x2∈[-2，2]，|f（x1）-f（x2）|≤k恒成立，则k的取值范围是（ ）
| A． | [e2-1，+∞） | B． | [e2，+∞） | C． | [e2+1，+∞） | D． | [1，+∞） |