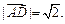题目内容
已知二面角 的平面角为
的平面角为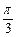 ,AB⊥BC,BC⊥CD,
,AB⊥BC,BC⊥CD, ,BC在l上,
,BC在l上, ,若
,若 ,则AD的长为 .
,则AD的长为 .
 的平面角为
的平面角为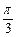 ,AB⊥BC,BC⊥CD,
,AB⊥BC,BC⊥CD, ,BC在l上,
,BC在l上, ,若
,若 ,则AD的长为 .
,则AD的长为 .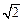
由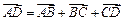 得:
得:
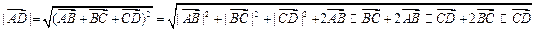
而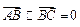 ,
,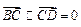 ,
,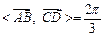 ,故
,故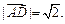
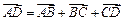 得:
得: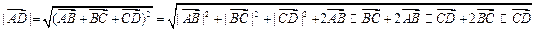
而
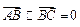 ,
,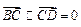 ,
,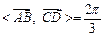 ,故
,故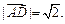

练习册系列答案
相关题目
题目内容
 的平面角为
的平面角为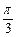 ,AB⊥BC,BC⊥CD,
,AB⊥BC,BC⊥CD, ,BC在l上,
,BC在l上, ,若
,若 ,则AD的长为 .
,则AD的长为 .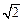
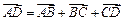 得:
得: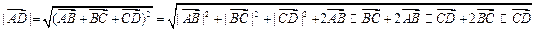
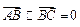 ,
,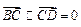 ,
,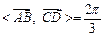 ,故
,故