题目内容
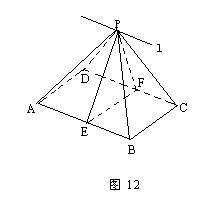
如图,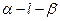 为60°的二面角,等腰直角三角形MPN的直角顶点P在l上,M∈α,N∈β,且MP与β所成的角等于NP与α所成的角.
为60°的二面角,等腰直角三角形MPN的直角顶点P在l上,M∈α,N∈β,且MP与β所成的角等于NP与α所成的角.
(1)求证: MN分别与α、β所成角相等;
(2)求MN与β所成角.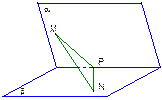
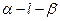 为60°的二面角,等腰直角三角形MPN的直角顶点P在l上,M∈α,N∈β,且MP与β所成的角等于NP与α所成的角.
为60°的二面角,等腰直角三角形MPN的直角顶点P在l上,M∈α,N∈β,且MP与β所成的角等于NP与α所成的角.(1)求证: MN分别与α、β所成角相等;
(2)求MN与β所成角.

(1) 证明略(2) MN与β所成角为30°
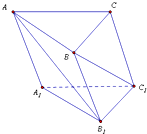
作NA⊥α于A,MB⊥β于B,连接AP、PB、BN、AM,再作AC⊥l于C,BD⊥l于D,连接NC、MD.
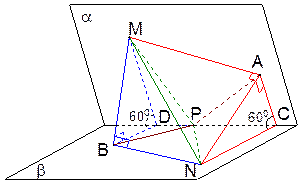
∵NA⊥α,MB⊥β,∴∠MPB、∠NPA分别是MP与β所成角及NP与α所成角,∠MNB,∠NMA分别是MN与β,α所成角,∴∠MPB=∠NPA.
在Rt△MPB与Rt△NPA中,PM=PN,∠MPB=∠NPA,∴△MPB≌△NPA,∴MB=NA.
在Rt△MNB与Rt△NMA中,MB=NA,MN是公共边,∴△MNB≌△NMA,∴∠MNB=∠NMA,即(1)结论成立.
(2)解:设∠MNB=θ,MN=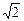 a,则PB=PN=a,MB=NA=
a,则PB=PN=a,MB=NA=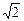 asinθ,NB=
asinθ,NB=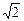 acosθ?,∵MB⊥β,BD⊥l,∴MD⊥l,∴∠MDB是二面角α—l—β的平面角,
acosθ?,∵MB⊥β,BD⊥l,∴MD⊥l,∴∠MDB是二面角α—l—β的平面角,
∴∠MDB=60°,同理∠NCA=60°,
∴BD=AC=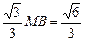 asinθ,CN=DM=
asinθ,CN=DM=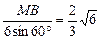 asinθ,
asinθ,
∵MB⊥β,MP⊥PN,∴BP⊥PN
∵∠BPN=90°,∠DPB=∠CNP,∴△BPD∽△PNC,∴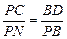
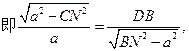
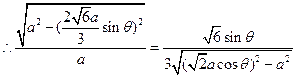
整理得,16sin4θ-16sin2θ+3=0
解得sin2θ=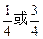 ,sinθ=
,sinθ=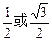 ,
,
当sinθ=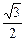 时,CN=
时,CN=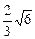 asinθ=
asinθ=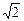 a>PN不合理,舍去.
a>PN不合理,舍去.
∴sinθ=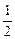 ,∴MN与β所成角为30°.
,∴MN与β所成角为30°.

∵NA⊥α,MB⊥β,∴∠MPB、∠NPA分别是MP与β所成角及NP与α所成角,∠MNB,∠NMA分别是MN与β,α所成角,∴∠MPB=∠NPA.
在Rt△MPB与Rt△NPA中,PM=PN,∠MPB=∠NPA,∴△MPB≌△NPA,∴MB=NA.
在Rt△MNB与Rt△NMA中,MB=NA,MN是公共边,∴△MNB≌△NMA,∴∠MNB=∠NMA,即(1)结论成立.
(2)解:设∠MNB=θ,MN=
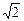 a,则PB=PN=a,MB=NA=
a,则PB=PN=a,MB=NA=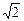 asinθ,NB=
asinθ,NB=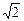 acosθ?,∵MB⊥β,BD⊥l,∴MD⊥l,∴∠MDB是二面角α—l—β的平面角,
acosθ?,∵MB⊥β,BD⊥l,∴MD⊥l,∴∠MDB是二面角α—l—β的平面角,∴∠MDB=60°,同理∠NCA=60°,
∴BD=AC=
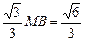 asinθ,CN=DM=
asinθ,CN=DM=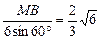 asinθ,
asinθ,∵MB⊥β,MP⊥PN,∴BP⊥PN
∵∠BPN=90°,∠DPB=∠CNP,∴△BPD∽△PNC,∴
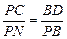
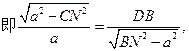
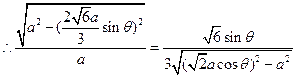
整理得,16sin4θ-16sin2θ+3=0
解得sin2θ=
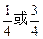 ,sinθ=
,sinθ=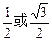 ,
,当sinθ=
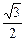 时,CN=
时,CN=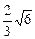 asinθ=
asinθ=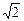 a>PN不合理,舍去.
a>PN不合理,舍去.∴sinθ=
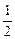 ,∴MN与β所成角为30°.
,∴MN与β所成角为30°.
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
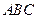 与正方形
与正方形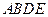 有一公共边
有一公共边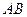 ,二面角
,二面角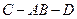 的余弦值为
的余弦值为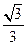 ,
,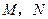 分别是
分别是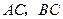 的中点,则
的中点,则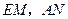 所成角的余弦值等于 。
所成角的余弦值等于 。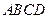 是直角梯形,角DABS是直角,
是直角梯形,角DABS是直角,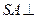 面
面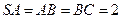 ,
,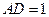 ,求面
,求面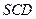 和面
和面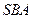 所成角的正切值.
所成角的正切值.
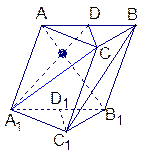
 .(1)求直线A1C与D1C1所成角的正切值;(2)在线段A1C上有一点Q,且C1Q=
.(1)求直线A1C与D1C1所成角的正切值;(2)在线段A1C上有一点Q,且C1Q= C1A1,求平面QDC与平面A1DC所成锐二面角的大小.
C1A1,求平面QDC与平面A1DC所成锐二面角的大小.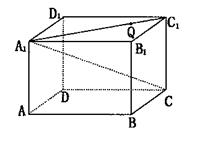
 -
- -
-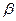 的棱
的棱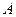 ,在平面
,在平面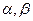 内各有一条射线
内各有一条射线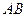 ,
,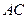 与
与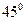 ,
,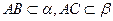 ,则
,则 。
。