题目内容
椭圆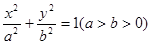 上的任意一点
上的任意一点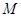 (除短轴端点除外)与短轴两个端点
(除短轴端点除外)与短轴两个端点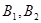 的连线交
的连线交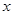 轴于点
轴于点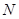 和
和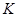 ,则
,则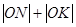 的最小值是
的最小值是
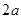
解析试题分析:求出椭圆上下顶点坐标,设P(xo,yo)K(xk,0)N(xn,0),利用K,P,B1三点共线求出K,N的横坐标,利用p在椭圆上,推出|OK|•|ON|=a2即可.
解:由椭圆方程知B1(0,-b),B2(0,b)另设P(xo,yo)K(xk,0)N(xn,0),由K,P,B1三点共线,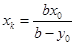 同理
同理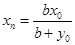 ,利用点在椭圆上,那么可知|OK|•|ON|=a2,即
,利用点在椭圆上,那么可知|OK|•|ON|=a2,即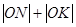 利用均值不等式可知其最小值为2a,故答案为2a
利用均值不等式可知其最小值为2a,故答案为2a
考点:向量共线,椭圆的性质
点评:本题是中档题,思路明确重点考查学生的计算能力,也可以由向量共线,或由直线方程截距式等求得点M坐标.

练习册系列答案
相关题目
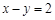 与抛物线
与抛物线 交于
交于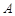 、
、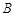 两点,则线段
两点,则线段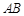 的中点坐标是______.
的中点坐标是______. 的焦点F的直线l与抛物线在第一象限的交点为A,直线l与抛物线的准线的交点为B,点A在抛物线的准线上的射影为C,若
的焦点F的直线l与抛物线在第一象限的交点为A,直线l与抛物线的准线的交点为B,点A在抛物线的准线上的射影为C,若 ,
, ,则抛物线的方程为 .
,则抛物线的方程为 . 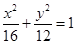 上的点到直线
上的点到直线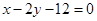 的距离的最小值为 。
的距离的最小值为 。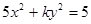 的一个焦点是
的一个焦点是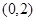 ,那么
,那么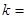 .
.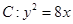 的焦点为
的焦点为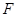 ,准线与
,准线与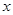 轴的交点为
轴的交点为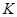 ,点
,点 在
在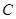 上且
上且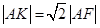 ,则
,则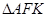 的面积为
的面积为 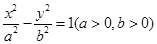 的一条渐近线的斜率为
的一条渐近线的斜率为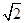 ,且右焦点与抛物线
,且右焦点与抛物线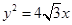 的焦点重合,则该双曲线的方程为 .
的焦点重合,则该双曲线的方程为 .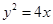 的焦点作直线
的焦点作直线 交抛物线于
交抛物线于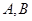 两点,若线段
两点,若线段 中点的横坐标为3,则
中点的横坐标为3,则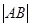 等于___________.
等于___________. 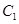 :
: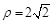 和曲线
和曲线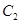 :
: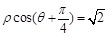 ,则
,则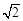 的点的个数为 .
的点的个数为 .