题目内容
设函数f(x)=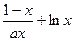 在[1+,∞
在[1+,∞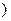 上为增函数.
上为增函数.
(1)求正实数a的取值范围.
(2)若a=1,求征: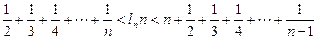 (n∈N*且n≥2)
(n∈N*且n≥2)
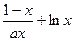 在[1+,∞
在[1+,∞ 上为增函数.
上为增函数. (1)求正实数a的取值范围.
(2)若a=1,求征:
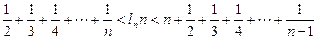 (n∈N*且n≥2)
(n∈N*且n≥2)(1)a≥1
(2)证明见解析
(2)证明见解析
(1)由已知:
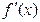 =
=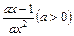
依题意得:
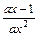 ≥0对x∈[1,+∞
≥0对x∈[1,+∞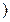 恒成立
恒成立∴ax-1≥0对x∈[1,+∞
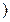 恒成立 ∴a-1≥0即:a≥1
恒成立 ∴a-1≥0即:a≥1(2)∵a="1 " ∴由(1)知:f(x)=
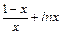 在[1,+∞
在[1,+∞ 上为增函数,
上为增函数,∴n≥2时:f(
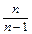 )=
)=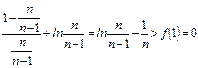
即:
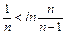
∴
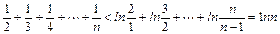
设g(x)=lnx-x x∈[1,+∞
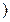 , 则
, 则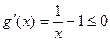 对
对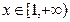 恒成立,
恒成立,∴g′(x)在[1+∞
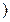 为减函数
为减函数∴n≥2时:g(
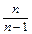 )=ln
)=ln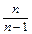 -
-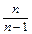 <g(1)=-1<0
<g(1)=-1<0 即:ln
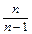 <
<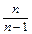 =1+
=1+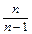 (n≥2)
(n≥2)∴
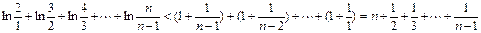
综上所证:
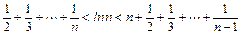 (n∈N*且≥2)成立.
(n∈N*且≥2)成立. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
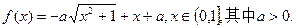
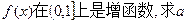 的取值范围;
的取值范围;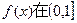 上的最大值.
上的最大值. 的图像关于原点中心对称,则
的图像关于原点中心对称,则 ( )
( ) 上为增函数
上为增函数 上为增函数,在
上为增函数,在 上为减函数
上为减函数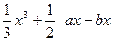 (a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).
(a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).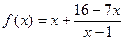 ,函数
,函数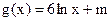 .
.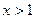 时,求函数f(x)的最小值;
时,求函数f(x)的最小值; 是可导函数)
是可导函数) ;
; 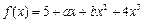 在
在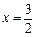 及
及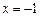 处有极值,
处有极值,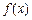 的极值;
的极值;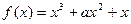 ,
,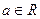 是常数,
是常数,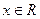 .
.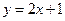 是曲线
是曲线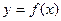 的一条切线,求
的一条切线,求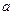 的值;
的值;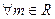 ,试证明
,试证明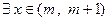 ,使
,使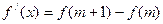 .
.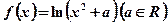 . (1)求在函数
. (1)求在函数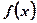 图像上点
图像上点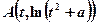 处的切线
处的切线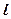 的方程;(2)若切线
的方程;(2)若切线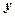 轴上的纵坐标截距记为
轴上的纵坐标截距记为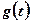 ,讨论
,讨论