题目内容
设函数g(x)=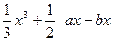 (a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).
(a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).
(1)若方程f(x)=0有两个实根分别为一2和4,求f(x)的表达式;
(2)若g(x)在区间[一1,3]上是单调递减函数,求a2+b2的最小值.
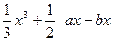 (a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).
(a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).(1)若方程f(x)=0有两个实根分别为一2和4,求f(x)的表达式;
(2)若g(x)在区间[一1,3]上是单调递减函数,求a2+b2的最小值.
(1)f(x)= x2-2x-8(2)13
(1)根据导数的几何意义知f(x)=g′(x)=x2+ax-b
由已知一2、4是方程x2+ax-b =0的两个实根-
由韦达定理,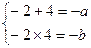 ,∴
,∴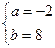 ,f(x)= x2-2x-8
,f(x)= x2-2x-8
(2)g(x)在区间【-1.3】上是单调递减函数,所以在【-1,3】区间上恒有
f(x)=g’(x)=x2+ax-b≤0,即f(x)=g’(x)=x2+ax-b≤0在【-1,3】恒成立,
这只需要满足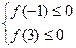 即可,也即
即可,也即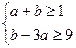
而a2+b2可以视为平面区域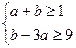 内的点到原点距离的平方,其中点(-2,3)距离原点最近,所以当
内的点到原点距离的平方,其中点(-2,3)距离原点最近,所以当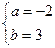 时,a2+b2有最小值13
时,a2+b2有最小值13
由已知一2、4是方程x2+ax-b =0的两个实根-
由韦达定理,
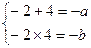 ,∴
,∴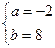 ,f(x)= x2-2x-8
,f(x)= x2-2x-8 (2)g(x)在区间【-1.3】上是单调递减函数,所以在【-1,3】区间上恒有
f(x)=g’(x)=x2+ax-b≤0,即f(x)=g’(x)=x2+ax-b≤0在【-1,3】恒成立,
这只需要满足
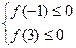 即可,也即
即可,也即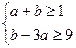
而a2+b2可以视为平面区域
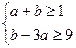 内的点到原点距离的平方,其中点(-2,3)距离原点最近,所以当
内的点到原点距离的平方,其中点(-2,3)距离原点最近,所以当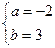 时,a2+b2有最小值13
时,a2+b2有最小值13
练习册系列答案
相关题目
 (b、c为常数).
(b、c为常数).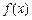 在
在
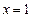 和
和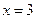 处取得极值,试求
处取得极值,试求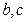 的值;
的值;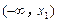 、
、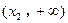 上单调递增,且在
上单调递增,且在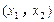 上单调递减,又满足
上单调递减,又满足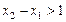 ,求证:
,求证: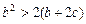 。
。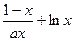 在[1+,∞
在[1+,∞ 上为增函数.
上为增函数. 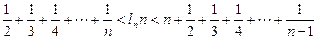 (n∈N*且n≥2)
(n∈N*且n≥2)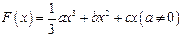 且
且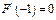
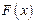 在
在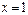 取得极小值-2,求函数
取得极小值-2,求函数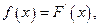 若
若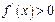 的解集为A,且
的解集为A,且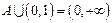 ,求
,求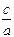 的范围
的范围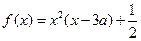 (
(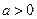 ,
,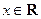 ).
).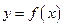 的极值;
的极值; (Ⅱ)若函数
(Ⅱ)若函数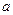 的取值范围.
的取值范围.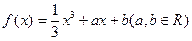 在
在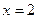 处取得的极小值是
处取得的极小值是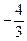 .
.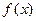 的单调递增区间;
的单调递增区间;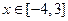 时,有
时,有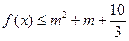 恒成立,求实数
恒成立,求实数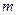 的取值范围.
的取值范围.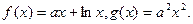
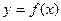 图像上的点到直线
图像上的点到直线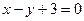 距离的最小值;
距离的最小值;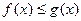 对一切正实数x都成立?若存在,求出a的取值范围;若不存在,请说明理由
对一切正实数x都成立?若存在,求出a的取值范围;若不存在,请说明理由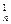 +2C
+2C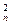 +3C
+3C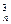 +…+nC
+…+nC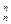 ,(n∈N*)
,(n∈N*) ,
, ;
; ,
,