题目内容
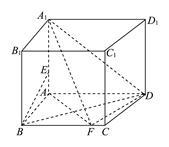
(本小题满分14分)已知在直四棱柱ABCDA1B1C1D1中,底面ABCD为直角梯形,且满足AD⊥AB,BC∥AD,AD=16,AB=8,BB1=8,E,F分别是线段A1A,BC上的点.
(1) 若A1E=5,BF=10,求证:BE∥平面A1FD.
(2) 若BD⊥A1F,求三棱锥A1AB1F的体积.
(1) 若A1E=5,BF=10,求证:BE∥平面A1FD.
(2) 若BD⊥A1F,求三棱锥A1AB1F的体积.

(1) 过E作EG∥AD交A1D于G,连接GF.
∵=,∴=,∴EG=10=BF.
∵BF∥AD,EG∥AD,∴BF∥EG.
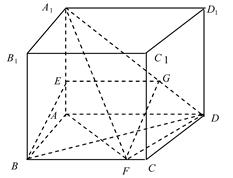
∴四边形BFGE是平行四边形.
∴BE∥FG.(4分)
又FG?平面A1FD,BE?平面A1FD,
∴BE∥平面A1FD.(6分)
(2) ∵在直四棱柱ABCDA1B1C1D1中,A1A⊥平面ABCD,BD?平面ABCD,∴A1A⊥BD.
由已知,BD⊥A1F,AA1∩A1F=A1,
∴BD⊥平面A1AF.
∴BD⊥AF.(8分)
∵梯形ABCD为直角梯形,且满足AD⊥AB,BC∥AD,
∴在Rt△BAD中,tan∠ABD==2.
在Rt△ABF中,tan∠BAF==.
∵BD⊥AF,∴∠ABD+∠BAF =,
=,
∴=,BF=4.(10分)
∵在直四棱柱ABCDA1B1C1D1中,A1A⊥平面ABCD,∴平面AA1B1B⊥平面ABCD,
又平面ABCD∩平面AA1B1B=AB,∠ABF=90°,
∴FB⊥平面AA1B1B,即BF为三棱锥FA1B1A的高.(12分)
∵∠AA1B1=90°,AA1=BB1=8,A1B1=AB=8,
∴S△AA1B1=32.
∴V三棱锥A1AB1F=V三棱锥FA1B1A=×S△AA1B1×BF=.(14分)
∵=,∴=,∴EG=10=BF.
∵BF∥AD,EG∥AD,∴BF∥EG.

∴四边形BFGE是平行四边形.
∴BE∥FG.(4分)
又FG?平面A1FD,BE?平面A1FD,
∴BE∥平面A1FD.(6分)
(2) ∵在直四棱柱ABCDA1B1C1D1中,A1A⊥平面ABCD,BD?平面ABCD,∴A1A⊥BD.
由已知,BD⊥A1F,AA1∩A1F=A1,
∴BD⊥平面A1AF.
∴BD⊥AF.(8分)
∵梯形ABCD为直角梯形,且满足AD⊥AB,BC∥AD,
∴在Rt△BAD中,tan∠ABD==2.
在Rt△ABF中,tan∠BAF==.
∵BD⊥AF,∴∠ABD+∠BAF
 =,
=,∴=,BF=4.(10分)
∵在直四棱柱ABCDA1B1C1D1中,A1A⊥平面ABCD,∴平面AA1B1B⊥平面ABCD,
又平面ABCD∩平面AA1B1B=AB,∠ABF=90°,
∴FB⊥平面AA1B1B,即BF为三棱锥FA1B1A的高.(12分)
∵∠AA1B1=90°,AA1=BB1=8,A1B1=AB=8,
∴S△AA1B1=32.
∴V三棱锥A1AB1F=V三棱锥FA1B1A=×S△AA1B1×BF=.(14分)
略

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
 的正方体
的正方体 中,异面直线
中,异面直线 与
与 所成的角等于( )
所成的角等于( )


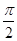

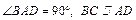 ,且PA=AB=BC=1,AD=2.
,且PA=AB=BC=1,AD=2.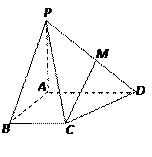
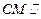 平面PAB;
平面PAB; 中,
中,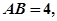 沿对角线
沿对角线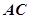 将正方形
将正方形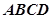 折成一个直二面角
折成一个直二面角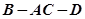 ,则点
,则点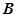 到直线
到直线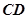 的距离为( )
的距离为( )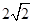
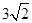
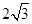
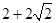
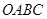 的三条棱
的三条棱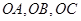 两两垂直,
两两垂直,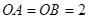 ,
,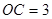 ,
,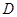 为四面体
为四面体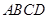 有三个面是直角三角形
有三个面是直角三角形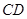 与
与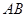 垂直并且相等
垂直并且相等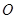 在四面体
在四面体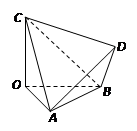
 C1的体积;
C1的体积;