题目内容
如图,直二面角D—AB—E中,四 边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.

(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求点D到平面ACE的距离。
 边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求点D到平面ACE的距离。
(Ⅰ)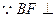 平面ACE.
平面ACE. 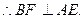
∵二面角D—AB—E为直二面角,且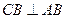 ,
,
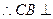 平面ABE.
平面ABE.
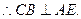
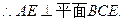
(Ⅱ)过点E作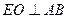 交AB于点O. OE=1.
交AB于点O. OE=1.
∵二面角D—AB—E为直二面角,∴EO⊥平面ABCD.
设D到平面ACE的距离为h,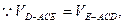

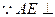 平面BCE,
平面BCE,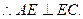
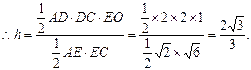
∴点D到平面ACE的距离为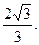
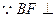 平面ACE.
平面ACE. 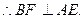
∵二面角D—AB—E为直二面角,且
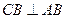 ,
,
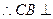 平面ABE.
平面ABE.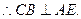
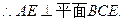
(Ⅱ)过点E作
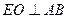 交AB于点O. OE=1.
交AB于点O. OE=1.∵二面角D—AB—E为直二面角,∴EO⊥平面ABCD.
设D到平面ACE的距离为h,
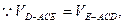

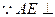 平面BCE,
平面BCE,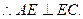
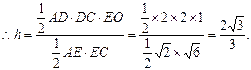
∴点D到平面ACE的距离为
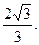
略

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
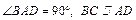 ,且PA=AB=BC=1,AD=2.
,且PA=AB=BC=1,AD=2.
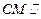 平面PAB;
平面PAB;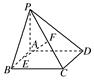
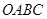 的三条棱
的三条棱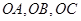 两两垂直,
两两垂直,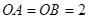 ,
,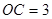 ,
,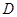 为四面体
为四面体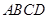 有三个面是直角三角形
有三个面是直角三角形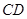 与
与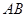 垂直并且相等
垂直并且相等 在四面体
在四面体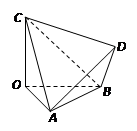
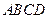 的边长为
的边长为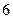 ,
,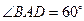 ,
,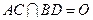 .将菱形
.将菱形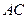 折起,使
折起,使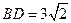 ,得到三棱锥
,得到三棱锥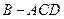 .
.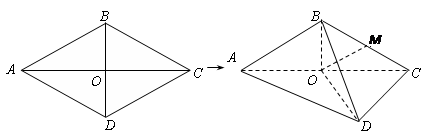
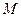 是棱
是棱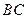 的中点,求证:
的中点,求证: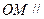 平面
平面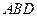 ;
;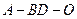 的余弦值;
的余弦值;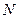 是线段
是线段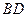 上一个动点,试确定
上一个动点,试确定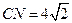 ,并证明你的结论.
,并证明你的结论. ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积 C1的体积;
C1的体积;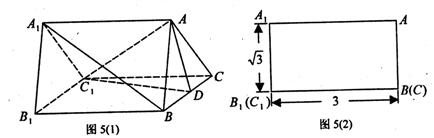
 CB⊥AB,AB=AD=
CB⊥AB,AB=AD= a,CD=
a,CD=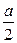 ,点E,F分别为线段AB,CD的中点,则EF=" " .
,点E,F分别为线段AB,CD的中点,则EF=" " .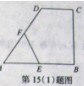
 )
)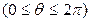 中,曲线
中,曲线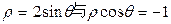 的交点的极坐标为 .
的交点的极坐标为 .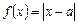 .若不等式
.若不等式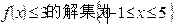 ,则实数
,则实数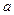 的值为 .
的值为 .