题目内容
已知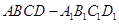 是底面边长为1的正四棱柱,高
是底面边长为1的正四棱柱,高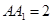 。求:
。求:
⑴异面直线 与
与 所成的角的大小(结果用反三角函数表示);
所成的角的大小(结果用反三角函数表示);
⑵四面体 的体积。
的体积。
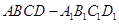 是底面边长为1的正四棱柱,高
是底面边长为1的正四棱柱,高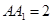 。求:
。求:⑴异面直线
 与
与 所成的角的大小(结果用反三角函数表示);
所成的角的大小(结果用反三角函数表示);⑵四面体
 的体积。
的体积。(1)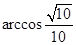
(2)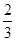
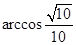
(2)
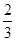
解:⑴连 ,∵
,∵  ,
,
∴异面直线 与
与 所成角为
所成角为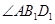 ,记
,记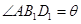 ,
,
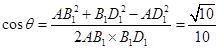
∴ 异面直线 与
与 所成角为
所成角为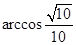 。
。
⑵连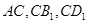 ,则所求四面体的体积
,则所求四面体的体积
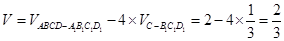 。
。
 ,∵
,∵  ,
,∴异面直线
 与
与 所成角为
所成角为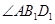 ,记
,记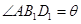 ,
,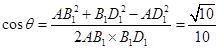
∴ 异面直线
 与
与 所成角为
所成角为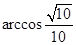 。
。⑵连
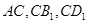 ,则所求四面体的体积
,则所求四面体的体积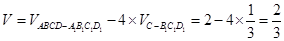 。
。
练习册系列答案
相关题目
 中,
中, ,又
,又 ⊥平面
⊥平面 .
. 上存在一点
上存在一点 ,使
,使 ,
, 的取值范围;
的取值范围; 的余弦值.
的余弦值.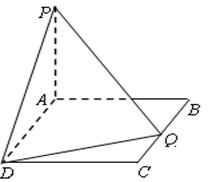

 中,
中,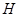 是正方形
是正方形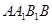 的中心,
的中心,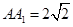 ,
,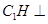 平面
平面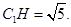
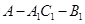 的正弦值;
的正弦值;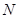 为棱
为棱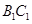 的中点,点
的中点,点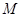 在平面
在平面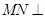 平面
平面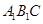 ,求线段
,求线段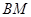 的长.
的长.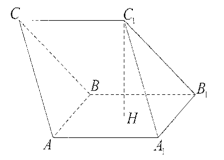
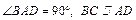 ,且PA=AB=BC=1,AD=2.
,且PA=AB=BC=1,AD=2.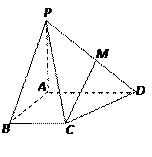
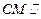 平面PAB;
平面PAB; ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积 C1的体积;
C1的体积;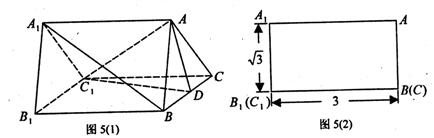
 CB⊥AB,AB=AD=
CB⊥AB,AB=AD= a,CD=
a,CD=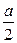 ,点E,F分别为线段AB,CD的中点,则EF=" " .
,点E,F分别为线段AB,CD的中点,则EF=" " .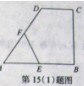
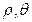 )
)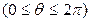 中,曲线
中,曲线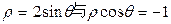 的交点的极坐标为 .
的交点的极坐标为 .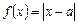 .若不等式
.若不等式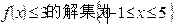 ,则实数
,则实数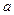 的值为 .
的值为 .