题目内容
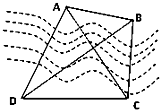
如图,A、B两点都在河的对岸(不可到达),为了测量A、B两点间的距离,选取一条基线CD,A、B、C、D在一平面内.测得:CD=200m,∠ADB=∠ACB=30°,∠CBD=60°,则AB=( )
A.
| B.200
| ||||||
C.100
| D.数据不够,无法计算 |

如图所示,∵∠ADB=∠ACB=30°,∠CBD=60°,∴AC⊥BD.
设AC∩BD=O,则△AOD∽△BOC,∴OC=OD,△OCD为等腰直角三角形,
∴∠ODC=∠OCS=45°,∴OC=OD=
CD=
×200=100
.
△BCO中,由tan∠ACB=tan30°=
=
=
,∴OB=
,
同理求得OA=
.
∴AB=
=
,
故选:A.
设AC∩BD=O,则△AOD∽△BOC,∴OC=OD,△OCD为等腰直角三角形,
∴∠ODC=∠OCS=45°,∴OC=OD=
| ||
| 2 |
| ||
| 2 |
| 2 |
△BCO中,由tan∠ACB=tan30°=
| ||
| 3 |
| OB |
| OC |
| OB | ||
100
|
100
| ||
| 3 |
同理求得OA=
100
| ||
| 3 |
∴AB=
| OA2+OB2 |
200
| ||
| 3 |
故选:A.

练习册系列答案
相关题目
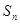 为数列
为数列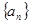 的前n项和,若
的前n项和,若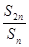
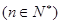 是非零常数,则称该数列为“和等比数列”.若数列
是非零常数,则称该数列为“和等比数列”.若数列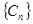 是首项为
是首项为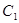 ,公差为
,公差为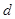 (
(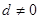 )的等差数列,且数列
)的等差数列,且数列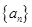 中,前n项和为
中,前n项和为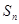 ,若
,若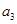 +
+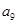 =6,则
=6,则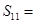 ( )
( )