题目内容
已知数列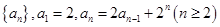
⑴求证: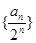 为等差数列;
为等差数列;
⑵求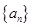 的前n项和
的前n项和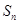 ;
;
⑶若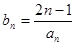 ,求数列
,求数列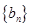 中的最大值.
中的最大值.
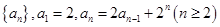
⑴求证:
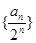 为等差数列;
为等差数列;⑵求
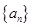 的前n项和
的前n项和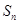 ;
;⑶若
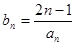 ,求数列
,求数列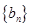 中的最大值.
中的最大值.⑴见解析;⑵Sn= (n-1)·2n+1+2;⑶最大值为b1=0.5.
试题分析:⑴利用等差数列的定义,研究
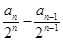 为定值;
为定值;⑵由⑴进一步得
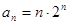 ,利用“错位相减法”求和.
,利用“错位相减法”求和.根据Sn=1·21+2·22+3·23+ +(n-1)·2n-1+n·2n
2Sn=1·22+2·23+3·23+ +(n-1)·2n+n·2n+1
两式相减得:-Sn=21+22+23+ +2n-n·2n+1 =
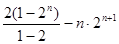
⑶由
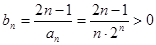
研究
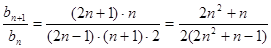 ,得到
,得到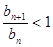 推出{bn}为递减数列
推出{bn}为递减数列数列{bn}中的最大值为b1.
试题解析:⑴∵
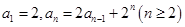
∴
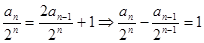
∴
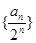 为等差数列,首项为
为等差数列,首项为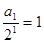 ,公差d=1 (4分)
,公差d=1 (4分)⑵由⑴得
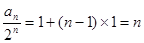 ∴
∴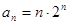 (6分)
(6分)∴Sn=1·21+2·22+3·23+ +(n-1)·2n-1+n·2n
2Sn=1·22+2·23+3·23+ +(n-1)·2n+n·2n+1
两式相减得:-Sn=21+22+23+ +2n-n·2n+1
=
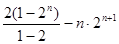
∴Sn=2-2n+1+n·2n+1=(n-1)·2n+1+2 (10分)
⑶
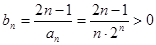
∴
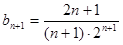 ∴
∴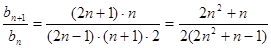 (12分)
(12分)又∵2(2n2+n-1)-(2n2+n)=2n2+n-2
当n≥1时,2n2+n-2>0 ∴2(2n2+n-1)>2n2+n>0
∴
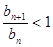 即bn+1<bn
即bn+1<bn∴{bn}为递减数列 (14分)
数列{bn}中的最大值为b1=0.5

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
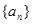 ,满足
,满足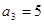 且
且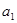 ,
,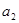 ,
,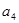 成等比数列.
成等比数列.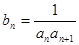 ,求数列
,求数列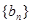 前
前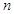 项的和为
项的和为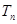 .
.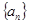 ( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.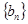 是等差数列;
是等差数列;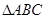 中,角
中,角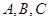 的对边分别为
的对边分别为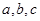 ,且
,且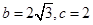 ,求
,求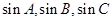 成等比数列,试判断
成等比数列,试判断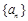 的首项
的首项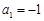 ,公差
,公差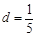 ,则
,则



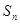 为数列
为数列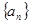 的前n项和,若
的前n项和,若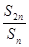
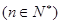 是非零常数,则称该数列为“和等比数列”.若数列
是非零常数,则称该数列为“和等比数列”.若数列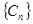 是首项为
是首项为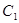 ,公差为
,公差为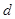 (
(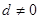 )的等差数列,且数列
)的等差数列,且数列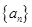 中,前n项和为
中,前n项和为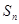 ,若
,若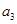 +
+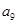 =6,则
=6,则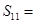 ( )
( )