题目内容
如图所示在△ABC中,sin2A+sin2C=sin2B+sinA.sinC
(1)求B的度数.
(2)设H为△ABC的垂心,且
•
=6求AC边长的最小值.
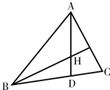
(1)求B的度数.
(2)设H为△ABC的垂心,且
| BH |
| BC |

(1)由sin2A+sin2C=sin2B+sinA.sinC,
利用正弦定理化简得:a2+c2=b2+ac,①
则根据余弦定理得:cosB=
∴cosB=
,由B∈(0,180°),
得到:B=60°;
(2)6=
•
=/
/•/
/•cos∠CBH=/
/•/
/=
/
/•/
/=
ac
∴ac=12
∴b2=a2+c2-ac≥2ac-ac=ac=12
∴bmin=2
利用正弦定理化简得:a2+c2=b2+ac,①
则根据余弦定理得:cosB=
| a2+c2-b2 |
| 2ac |
∴cosB=
| 1 |
| 2 |
得到:B=60°;
(2)6=
| BH |
| BC |
| BH |
| BC |
| BD |
| BC |
| 1 |
| 2 |
| AB |
| BC |
| 1 |
| 2 |
∴ac=12
∴b2=a2+c2-ac≥2ac-ac=ac=12
∴bmin=2
| 3 |

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
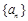 的首项
的首项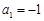 ,公差
,公差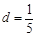 ,则
,则


