题目内容
3.已知函数f(x)满足f(x-3)=$\frac{x}{{x}^{2}+1}$.(1)求函数的解析式;
(2)求函数f(x)的值域.
分析 (1)利用换元法求出函数f(x)的解析式即可;(2)先求出函数的导数,得到函数的单调区间,从而求出函数的值域.
解答 解:(1)令z=x-3,则x=z+3,
∴f(z)=$\frac{z+3}{{(z+3)}^{2}+1}$,
∴f(x)=$\frac{x+3}{{x}^{2}+6x+10}$;
(2)f′(x)=-$\frac{(x+2)(x+4)}{{x}^{2}+6x+10}$,
令f′(x)>0,解得:-4<x<-2,
令f′(x)<0,解得:x>-2或x<-4,
∴f(x)在(-∞,-4),(-2,+∞)递减,在(-4,-2)递增,
又∵f(x)=$\frac{x+3}{{x}^{2}+6x+10}$=$\frac{1+\frac{3}{x}}{x+6+\frac{10}{x}}$,
当x→+∞时,f(x)→0,
当x→-∞时,f(x)→0,
∴函数f(x)的大致图象如图所示: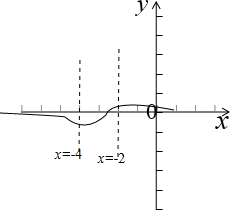 ,
,
∴f(x)最大值=f(x)极大值=f(-2)=$\frac{1}{2}$,
f(x)最小值=f(x)极小值=f(-4)=-$\frac{1}{2}$,
∴函数f(x)的值域是:[-$\frac{1}{2}$,$\frac{1}{2}$].
点评 本题考察了函数的解析式问题,考察函数的值域问题,本题是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知M(3,-2),N(-5,-1),若$\overrightarrow{MP}=\frac{1}{2}\overrightarrow{MN}$,则P点的坐标为( )
| A. | (-8,1) | B. | (8,-1) | C. | $(-1,-\frac{3}{2})$ | D. | $(1,\frac{3}{2})$ |
14.若实数a,b,c满足|a-c|<|b|,则下列不等式中成立的是( )
| A. | |a|>|b|-|c| | B. | |a|<|b|+|c| | C. | a>c-b | D. | a<b+c |
11.设函数f(x)=$\frac{1}{3}$x3-2f′(0)ex+3x-1,则f(0)=( )
| A. | -3 | B. | 3 | C. | -1 | D. | 5 |
12. 如图所示,P、Q为△ABC内的两点,且$\overrightarrow{AP}$=$\frac{2}{5}$$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$,$\overrightarrow{AQ}$=$\frac{5}{3}$$\overrightarrow{AP}$-$\frac{1}{12}$$\overrightarrow{AC}$,则△ABP的面积与△ABQ的面积之比为( )
如图所示,P、Q为△ABC内的两点,且$\overrightarrow{AP}$=$\frac{2}{5}$$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$,$\overrightarrow{AQ}$=$\frac{5}{3}$$\overrightarrow{AP}$-$\frac{1}{12}$$\overrightarrow{AC}$,则△ABP的面积与△ABQ的面积之比为( )
 如图所示,P、Q为△ABC内的两点,且$\overrightarrow{AP}$=$\frac{2}{5}$$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$,$\overrightarrow{AQ}$=$\frac{5}{3}$$\overrightarrow{AP}$-$\frac{1}{12}$$\overrightarrow{AC}$,则△ABP的面积与△ABQ的面积之比为( )
如图所示,P、Q为△ABC内的两点,且$\overrightarrow{AP}$=$\frac{2}{5}$$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$,$\overrightarrow{AQ}$=$\frac{5}{3}$$\overrightarrow{AP}$-$\frac{1}{12}$$\overrightarrow{AC}$,则△ABP的面积与△ABQ的面积之比为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{3}$ |
13.若tanα=$\frac{4}{3}$,且α为第三象限角,则sinα=( )
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |