题目内容
12. 如图所示,P、Q为△ABC内的两点,且$\overrightarrow{AP}$=$\frac{2}{5}$$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$,$\overrightarrow{AQ}$=$\frac{5}{3}$$\overrightarrow{AP}$-$\frac{1}{12}$$\overrightarrow{AC}$,则△ABP的面积与△ABQ的面积之比为( )
如图所示,P、Q为△ABC内的两点,且$\overrightarrow{AP}$=$\frac{2}{5}$$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$,$\overrightarrow{AQ}$=$\frac{5}{3}$$\overrightarrow{AP}$-$\frac{1}{12}$$\overrightarrow{AC}$,则△ABP的面积与△ABQ的面积之比为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{3}$ |
分析 分别设出$\overrightarrow{AM}$和$\overrightarrow{AN}$,进而根据四边形法则确定三角形ABP和三角形ABC,以及三角形ABQ和三角形APQ的比例关系,进而求得答案.
解答 解: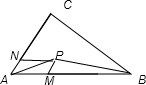
设$\overrightarrow{AM}$=$\frac{2}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{1}{5}$$\overrightarrow{AC}$
则 $\overrightarrow{AP}$=$\overrightarrow{AM}$$+\overrightarrow{AN}$
由平行四边形法则知NP∥AB
所以 $\frac{{S}_{△ABP}}{{S}_{△ABC}}$$\frac{|\overrightarrow{AN|}}{|\overrightarrow{AC|}}$$\frac{1}{5}$,
同理 $\frac{{S}_{△ABQ}}{{S}_{△ABC}}$=$\frac{1}{4}$
故 $\frac{{S}_{△ABP}}{{S}_{△ABQ}}$=$\frac{4}{5}$,
故选C.
点评 本题主要考查了平面向量的应用.用向量解决几何问题的步骤:建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面问题转化为向量问题;
通过向量运算,研究几何元素之间的关系,如:距离,夹角等,把运算结果“翻译”成几何关系.

练习册系列答案
相关题目
20.某企业工会对清明假期在省内旅游的职工进行统计,用分层抽样的方法从去汉中、安康、延安、渭南、宝鸡五地旅游人员中抽取若干人成立旅游爱好者协会,相关数据统计如下:
(Ⅰ)求a,b,c,d的值;
(Ⅱ)若从去延安和宝鸡两地抽取的人数中选2人担任旅游爱好者协会与工会之间的联络员,求这两人来自不同旅游地的概率.
| 旅游地 | 相关人数 | 抽取人数 |
| 汉中 | 30 | a |
| 安康 | b | 1 |
| 延安 | 24 | 4 |
| 渭南 | c | 3 |
| 宝鸡 | 12 | d |
(Ⅱ)若从去延安和宝鸡两地抽取的人数中选2人担任旅游爱好者协会与工会之间的联络员,求这两人来自不同旅游地的概率.
7.一段圆弧的长度等于其圆内接正方形的边长,则其圆心角的弧度数为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |