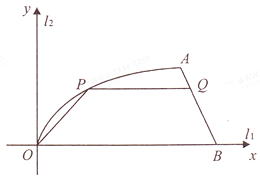
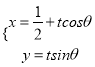题目内容
【题目】第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行，这是2017年我国重要的主场外交活动，对推动国际和地区合作具有重要意义．某高中政教处为了调查学生对“一带一路”的关注情况，在全校组织了“一带一路知多少”的知识问卷测试，并从中随机抽取了12份问卷，得到其测试成绩（百分制），如茎叶图所示．
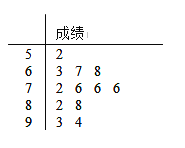
（1）写出该样本的众数、中位数，若该校共有3000名学生，试估计该校测试成绩在70分以上的人数；
（2）从所抽取的70分以上的学生中再随机选取4人．
①记
表示选取4人的成绩的平均数，求
；
②记
表示测试成绩在80分以上的人数，求
的分布和数学期望．
【答案】（1）
；（2）①
，②
.
【解析】试题分析：（1）众数为
，中位数为
，抽取的
人中， 
分以下的有
人，不低于
分的有
人，从而求出从该校学生中任选
人，这个人测试成绩在
分以上的概率，由此能求出该校这次测试成绩在
分以上的人数；（2）①由题意知
分以上的有
， 
， 
， 
， 
， 
， 
， 
，当所选取的四个人的成绩的平均分大于
分时，有两类：一类是： 
， 
， 
， 
，共1种；另一类是： 
， 
， 
， 
，共3种．由此能求出
；②由题意得
的可能取值为0，1，2，3，4，分别求出相应的概率，由此能求出
的分布列和
．
试题解析：(1)众数为76，中位数为76.抽取的12人中，70分以下的有4人，不低于70分的有8人，故从该校学生中人选1人，这个人测试成绩在70分以上的概率为
，故该校这次测试成绩在70分以上的约有
（人）
(2)①由题意知70分以上的有72，76，76，76，82，88，93，94.
当所选取的四个人的成绩的平均分大于87分时，有两类.
一类是82，88，93，94，共1种；
另一类是76，88，93，94，共3种.所以 
.
②由题意可得， 
的可能取值为0，1，2，3，4
,
,
,
,
.
的分别列为
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
.
