题目内容
【题目】如图,某小区内有两条互相垂直的道路![]() 与
与![]() ,平面直角坐标系
,平面直角坐标系![]() 的第一象限有一块空地
的第一象限有一块空地![]() ,其边界
,其边界![]() 是函数
是函数![]() 的图象,前一段曲线
的图象,前一段曲线![]() 是函数
是函数![]() 图象的一部分,后一段
图象的一部分,后一段![]() 是一条线段.测得
是一条线段.测得![]() 到
到![]() 的距离为8米,到
的距离为8米,到![]() 的距离为16米,
的距离为16米,![]() 长为20米.
长为20米.
(1)求函数![]() 的解析式;
的解析式;
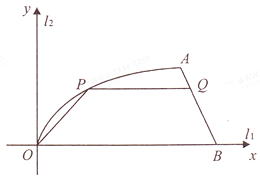
(2)现要在此地建一个社区活动中心,平面图为梯形![]() (其中
(其中![]() ,
,![]() 为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
【答案】(1)![]() ;(2)当梯形的高为
;(2)当梯形的高为![]() 米时,活动中心的占地面积最大,最大面积为
米时,活动中心的占地面积最大,最大面积为![]() 平方米
平方米
【解析】分析:(1)以![]() 代入
代入![]() ,得
,得![]() ,再由
,再由![]() ,
,![]() 两点可得直线
两点可得直线![]() ,从而利用分段函数表示即可;
,从而利用分段函数表示即可;
(2)设梯形的高为![]() 米,则
米,则![]() ,进而得
,进而得![]() ,梯形的面积
,梯形的面积![]() ,求导利用函数单调性求解最值即可.
,求导利用函数单调性求解最值即可.
详解:(1)以![]() 代入
代入![]() ,得
,得![]() ,
,
因为![]() ,得直线
,得直线![]() :
:![]() ,
,
所以![]() .
.
(2)设梯形的高为![]() 米,则
米,则![]() ,且
,且![]() ,
,![]() ,
,
所以![]() ,
,
所以梯形的面积![]() ,
,
由![]() ,
,
令![]() ,得
,得![]() ,列表如下:
,列表如下:
|
|
|
|
| + | 0 | - |
| ↗ | 极大值 | ↘ |
所以当![]() 时,
时,![]() 取得极大值,即为最大值为
取得极大值,即为最大值为![]() .
.
答:当梯形的高为![]() 米时,活动中心的占地面积最大,最大面积为
米时,活动中心的占地面积最大,最大面积为![]() 平方米.
平方米.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】改革开放四十周年纪念币从2018年12月5日起可以开始预约![]() 通过市场调查,得到该纪念章每1枚的市场价
通过市场调查,得到该纪念章每1枚的市场价![]() 单位:元
单位:元![]() 与上市时间
与上市时间![]() 单位:天
单位:天![]() 的数据如下:
的数据如下:
上市时间x天 | 8 | 10 | 32 |
市场价y元 | 82 | 60 | 82 |
![]() 根据上表数据,从下列函数:
根据上表数据,从下列函数:![]() ;
;![]() ;
;![]() 中选取一个恰当的函数刻画改革开放四十周年纪念章的市场价y与上市时间x的变化关系并说明理由
中选取一个恰当的函数刻画改革开放四十周年纪念章的市场价y与上市时间x的变化关系并说明理由
![]() 利用你选取的函数,求改革开放四十周年纪念章市场价最低时的上市天数及最低的价格.
利用你选取的函数,求改革开放四十周年纪念章市场价最低时的上市天数及最低的价格.